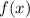 необходимо найти ноли производной
необходимо найти ноли производной 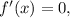 т.е. точки, где у функции будет экстремум, и показать, что до экстремума функция
т.е. точки, где у функции будет экстремум, и показать, что до экстремума функция 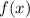 падает, т.е. производная
падает, т.е. производная 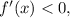 а после экстремума функция растёт, т.е. производная
а после экстремума функция растёт, т.е. производная 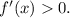
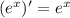 ;
;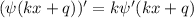 ;
;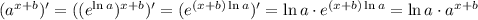 ;
;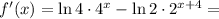
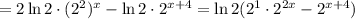 ;
;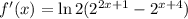 ;
;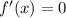 ;
; ;
;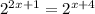 ;
;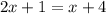 ;
;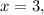 причём это единственный корень.
причём это единственный корень. например при
например при 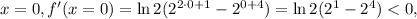 т.е. функция убывает.
т.е. функция убывает.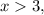 например при
например при 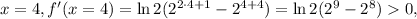 т.е. функция растёт.
т.е. функция растёт.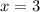 как раз достигается минимум:
как раз достигается минимум: 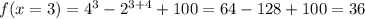 ;
;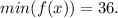
Объяснение:
Чтобы найти вероятность события А - " из двух деталей вынутых поочередно из первой и второй партий хотя бы одна - бракованная",найдем вероятность противоположного события В- "обе вынутые детали небракованные".
Вероятность вынуть небракованную деталь из первой партии равна 0,95.
Вероятность вынуть небракованную деталь из второй партии равна 0,96.
Вероятность события В равна произведению вероятностей,
р(В)=0,95·0,96=0,912.
Так как сумма противоположных событий равна 1, то
р(А)=1-р(В)=1-0, 912=0,088
1. Меньшая сторона детской площадки (ширина) равна: 16 м
Большая сторона детской площадки (длина) равна: 10 м
2. Необходимое количество упаковок равно: 3
Объяснение:
(1) Меньшая сторона - х
Большая сторона - х+6
Площадь: S = 160м^2
Х × (х+6) = 160
Х^2 + 6х - 160 = 0
D = b^2 - 4ac = 36 - (-640) = 36 + 640 = 676 = 26^2
X1 = (-b - корень из D) / 2a = (-6-26) /2 = -32/2
X1 = -16 ( -16 метров быть не может )
Х2 = (-b + корень из D) /2a = (-6+26) /2 = 20/2
X2 = 10
X + 6 = X2 + 6 = 10 + 6 = 16
(2) Р = 2 × (10 + 16) = 2 × 26 = 52
52 ÷ 20 = 2,6
2,6 ~ (до целых) 3
2^(x)=t
t^2-16t+100=0-парабола,ветки вниз.найдем координаты вершины:
t(min)=16/2=8
2^(x)=8
2^(x)=2^3
x=3
f(3)=64-128+100=36-наименьшее значение функции