Объяснение:
1. Найдите промежутки возрастания и убывания:
Найдем производную, приравняем к нулю, найдем корни.
Определим знаки производной на промежутках. Если "+", функция возрастает, "-" - убывает.
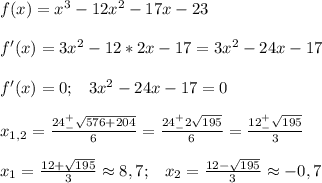
См. рис.
Функция возрастает при х ∈ [-∞; -0,7]∪[8,7; +∞]
или
![\displaystyle x\in [- \infty ;\;\frac{12-\sqrt{195} }{3} ]\cup [\frac{12+\sqrt{195} }{3};\;+ \infty ]](/tpl/images/4664/9108/8e18d.png)
Функция убывает при х ∈ [-0,7; 8,7]
или
![\displaystyle x\in[\frac{12-\sqrt{195} }{3};\;\frac{12+\sqrt{195} }{3} ]](/tpl/images/4664/9108/36d34.png)
2. Найдите стационарные точки:
Точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
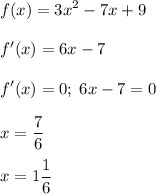
3. Найдите локальные максимумы и минимумы функции.
Найдем производную, приравняем к нулю, найдем корни.
Определим знаки производной на промежутках. Если производная меняет знак с "+" на "-", то будет точка максимума. Если производная меняет знак с "-" на "+" - точка минимума.
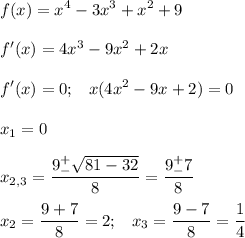
См. рис.

Объяснение:
1)Если две прямые параллельны, то при пересечении их с третьей секущей накрест лежащие углы равны.
При пересечении двух параллельных прямых третьей прямой, образованные ими соответственные углы равны
При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна 180°
2). Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
3)Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним
ΔАВС, ∠А=46°, внешний угол при вершине С равен 107°.
∠В=107°-46°=61°
Итак , обозначим числа k, l, m и n. d -шаг арифм. прогрессии, q - знаменатель прогрессии.
тогда получаем систему из 6 уравнений.
l=k+d
m=k+2d
m=lq
n=lq²
k+m=40
l+m=k+d+k+2d=2k+3d=20
Решаем эту систему
l=k+d
m=k+2d
m=lq=(k+d)q
n=lq²=(k+d)q²
k+m=k+lq²=k+(k+d)q²=40
l+m=k+d+k+2d=2k+3d=20
из последнего уравнения
Приравнивая второе и третье получим
k+2d=(k+d)q
из предпоследнего
3k(20+k)+(40-k)²=40*3(20+k)
60k+3k²+1600-80k+k²=2400-120k
4k²-140k-800=0
k²-35k=200
D=35²+4*200=2025
k₁=(35-45)/2=-5
k₂=(35+45)/2=40
d₁=(20-2*(-5))/3=10
l₁=-5+10=5
m₁=15
q₁=3
n₁=45
d₂=(20-2*40)/3=-20
l₂=40-20=20
m₂=0
q₂=0
n₂=0
ответ: два решения: -5,5,15,45 и 40, 20, 0, 0