и 
. Чтобы найти координату 
точек пересечения приравняем две функции (они пересекаются, значит приравниваем). Получаем:
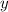можем найти подставив в выражение первой функции , а можно сделать проще. Так как пересечение будет с прямой , то и точки пересечения будут иметь координату . Итак, получилось две точки пересечения с координатами: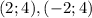 
.![[0;1]](/tpl/images/0561/5883/90495.png)
(этот отрезок по оси ), найдем значения 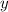на концах этого отрезка: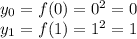
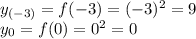
MK/КЕ-tg E; МК/МЕ-cos M; МК/МЕ-sin E; КЕ/МЕ-sin M; КЕ/МЕ- cosЕ
Объяснение:
МЕ-гипотенуза треугольника МЕК.
У ∠ Е - МК-противолежащий катет, КЕ- прилежащий катет, .
У ∠М- МК-прилежащий катет, КЕ- противолежащий катет. Решаем далее по правилам Определения тригонометрических функций.
Определения тригонометрических функций:
Синус угла ( sin α ) - отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α) - отношение прилежащего катета к гипотенузе.
Тангенс угла ( tg α ) - отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) - отношение прилежащего катета к противолежащему.