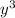 куб числа по модулю
куб числа по модулю 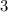 (остатки от деления) сравнимы с
(остатки от деления) сравнимы с 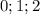 соответственно когда
соответственно когда 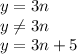 , где
, где 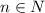 .
. 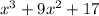
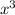 так же как
так же как 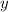 ,
,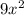 дает остаток
дает остаток 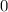 , число
, число 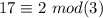 , то есть остаток числа
, то есть остаток числа 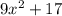 равен
равен 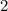 при делений на
при делений на 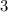 .
.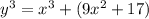
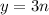 слева остаток всегда равен
слева остаток всегда равен 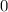 , но справа уже не может поэтому
, но справа уже не может поэтому 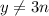
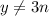 , слева остаток при делений на
, слева остаток при делений на 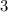 как ранее был сказан равен
как ранее был сказан равен  , но тогда справа должно быть число дающее
, но тогда справа должно быть число дающее 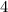 , а оно дает при делений на
, а оно дает при делений на 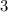 остаток
остаток  отсюда
отсюда 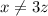 подходит
подходит 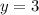
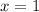
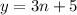 , но оно так же не действительно , то есть решение
, но оно так же не действительно , то есть решение 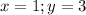
Решение:
Составим характеристическое уравнение
k² - 3k -10 = 0
D = 3² -4(-10) =49
Т.к. характеристическое уравнение имеет два корня,
и корни не имеют комплексный вид, то
решение соотв. дифференциального уравнения имеет вид:
Получаем окончательный ответ: