При каких значениях х: дробь (6-5х)/(х+25) принимает положительные значения?

👇

Увидеть ответ

Ответ:

Куколканупка

22.07.2020

(6-5х)/(х+25) и далее по картинке

При каких значениях х: дробь (6-5х)/(х+25) принимает положительные значения?

4,6(71 оценок)

Ответ:

Olka1909

22.07.2020

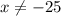
ОДЗ $x\neq-25$

Далее это равносильно (6-5x)*(x+25)>0

Первый множитель меняет знак при переходе через x=6/5=1.2 (6-5x=0 6=5x x=6/5)

Второй множитель меняет знак при переходе через x=-25 (x+25=0 x=-25)

Оба множителя в нечетной (первой) степени, значит при переходе через их корни выражение будет менять знак на противоположный.

Выясним знак при 0: (6-5*0)*(0+25)=6*25>0

Значит в интервале от -25 до 1,2 (где находится 0) это выражение будет принимать положительные значения.

ОТВЕТ (-25;1,2)

4,5(20 оценок)

Открыть все ответы

Ответ:

света8612

22.07.2020

Добрый день! Рассмотрим каждую функцию по отдельности и проведем их анализ на непрерывность.

1) Функция f(x) = 6^(1/(4-x)).

Для того, чтобы узнать, где функция непрерывна, мы должны рассмотреть два случая:
а) Проверить, нет ли разрыва функции внутри области определения (то есть, когда 4-x не равно 0).
б) Установить, является ли функция непрерывной на краях области определения (то есть, когда 4-x равно 0).

а) Проведем проверку разрыва внутри области определения функции. Для этого решим уравнение 4-x = 0. Получим x = 4. Таким образом, разрыва внутри области определения нет.

б) Теперь рассмотрим краевые точки области определения функции. Подставляя значения, близкие к x = 4, мы можем прийти к выводу, что функция будет непрерывна в x = 4.

Таким образом, функция f(x) = 6^(1/(4-x)) будет непрерывной на всей своей области определения.

Теперь построим схематический график функции:

|
|
|
|
|
----------------------+----
|
|
|
|
* x=4
|
|
|
|
|

2) Функция f(x) = система: cos(x), если х<=0; 2^x, если 02.

Анализируем функцию на непрерывность в каждой области определения:

а) Функция cos(x) непрерывна на всей числовой прямой, поэтому она будет непрерывной при х<=0.

б) Функция 2^x ограничена и строго возрастает на своей области определения (0
в) Функция f(x) = 4 есть постоянная функция, а постоянная функция непрерывна на всей числовой прямой. Поэтому функция f(x) = 4 будет непрерывной при x>2.

Таким образом, функция f(x) = система: cos(x), если х<=0; 2^x, если 02 непрерывна на всей своей области определения.

Теперь построим схематический график функции:

4|
|
|
|
|
|
|
--------------------+----
|
* x=2
|
|
|
|
* x=0
-------------------x=0

4,7(99 оценок)

Ответ:

саидолим

22.07.2020

Для решения данного уравнения, нам необходимо использовать свойства и формулы тригонометрии. Давайте разберем каждый шаг по порядку.

Первым шагом я бы разделил уравнение на корень (-7cosx):
(6sin^2x + 5sinx - 4) * корень (-7cosx) = 0
6sin^2x + 5sinx - 4 = 0

Далее, заметим, что это уравнение квадратное относительно sinx. Мы можем заменить sinx на переменную t и решить уравнение относительно t:

6t^2 + 5t - 4 = 0

Теперь, нам нужно решить это квадратное уравнение для t. Для этого, мы можем использовать формулу дискриминанта:
D = b^2 - 4ac

Где a = 6, b = 5 и c = -4. Подставляем значения в формулу:
D = 5^2 - 4 * 6 * -4
D = 25 + 96
D = 121

Как результат, получаем значение дискриминанта D = 121.

Так как дискриминант положительный, у нас есть два различных решения для t. Для их нахождения, мы можем использовать формулу корней квадратного уравнения:
t1,2 = (-b ± корень(D)) / (2a)

Подставляем значения a, b, и D в формулу:
t1,2 = (-5 ± корень(121)) / (2*6)
t1 = (-5 + 11) / 12
t1 = 6 / 12
t1 = 1/2

t2 = (-5 - 11) / 12
t2 = -16 / 12
t2 = -4/3

Таким образом, мы нашли два значения для t: t1 = 1/2 и t2 = -4/3.

Далее, нам нужно найти значения sinx, соответствующие этим значениям t. Для этого, мы можем воспользоваться соотношением sinx = t.

Итак, у нас есть два решения для sinx:
sinx = 1/2 и sinx = -4/3

Однако, синус x может быть только от -1 до 1, поэтому мы можем отбросить вариант sinx = -4/3, так как он выходит за допустимый диапазон.

Таким образом, мы получаем одно решение для sinx: sinx = 1/2.

Но мы хотим найти значения x, а не sinx. Чтобы найти x, мы можем использовать обратную функцию к синусу, а именно арксинус (или sin^-1 или asin).

Таким образом, мы можем записать ответ в виде:
x = arcsin(1/2)

Теперь, нам нужно найти значения арксинуса от 1/2. Это можно сделать с помощью таблиц или калькулятора.

Итак, x = arcsin(1/2). Это значит, что x является таким углом, при котором синус равен 1/2.

Из таблицы или калькулятора мы можем узнать, что существует два значения угла, при которых sin равен 1/2: x = 30° и x = 150°.

Таким образом, окончательные ответы для уравнения (6sin^2x + 5sinx - 4) * корень (-7cosx) = 0 это:
x = 30° и x = 150°.

4,6(57 оценок)

Это интересно:

Искусство-и-развлечения

20.08.2020

Школа дома: как не потеряться и организоваться...

Дом-и-сад

03.02.2020

Как быстро и эффективно избавиться от шоколадных пятен...

Хобби-и-рукоделие

07.07.2021

Как сделать светящуюся палочку: пошаговая инструкция...

Питомцы-и-животные