Точка n(-2; a) принадлежит графику функции y= -x²+3. найдите значение a. принадлежит ли графику данной - id481929920230203 от Варя1милаха 03.02.2023 05:09

Question

Алгебра: Точка n(-2; a) принадлежит графику функции y= -x²+3. найдите значение a. принадлежит ли графику данной функций точка m(3; 6a)?

Варя1милаха · Accepted Answer

Каноническое уравнение, задающее эллипс, выглядит так:

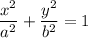
$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$

Перепишем уравнение эллипса, поменяв местами параметры и :

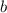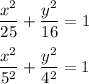
$\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\\\\\dfrac{x^2}{5^2}+\dfrac{y^2}{4^2}=1$

При этом мы получим конгруэнтный эллипс, только повёрнутый в системе координат на 90° (конгруэнтность следует из симметричности канонического уравнения). Поэтому он будет иметь тот же эксцентриситет и то же фокальное расстояние.

Найдём эксцентриситет:

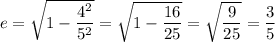
$e=\sqrt{1-\dfrac{4^2}{5^2}}=\sqrt{1-\dfrac{16}{25}}=\sqrt{\dfrac{9}{25}}=\dfrac{3}{5}$

Найдём фокальное расстояние (полурасстояние между фокусами):

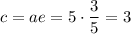
$c=ae=5 \cdot \dfrac{3}{5}=3$

Тогда расстояние между фокусами в два раза больше: 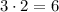$3 \cdot 2=6$ .

ответ: 6 ед.

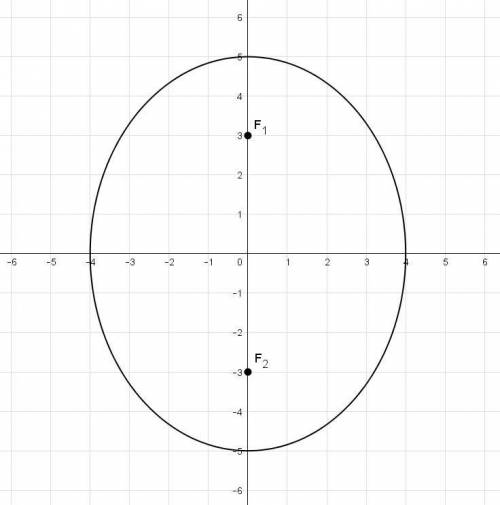
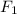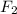На чертеже изображён данный эллипс. F_1 и F_2 — его фокусы.

Найти расстояние между фокусами эллипса<img src=

" />

Точка n(-2; a) принадлежит графику функции y= -x²+3. найдите значение a. принадлежит ли графику данной функций точка m(3; 6a)?

MOGZ ответил