Решите неравенство : x^2-49< 0 (никак не могу понять как решать после (x-7)(x+7)< 0)

👇

Увидеть ответ

Ответ:

Maксим56

02.03.2022

Тебе надо 49 перенести через знак<
получится: х²<49
и теперь: х<7 или х<-7

4,6(48 оценок)

Открыть все ответы

Ответ:

linaaaa2Li

02.03.2022

Объяснение:

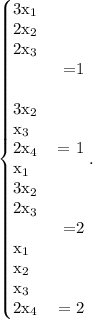
$\left\{\begin{array}{}3x_1&2x_2&2x_3& \ \ \ \ \ \ =1\\&3x_2&x_3&2x_4\ \ =1\\x_1&3x_2&2x_3&\ \ \ \ \ \ \ \ =2\\x_1&x_2&x_3&2x_4\ \ \ =2\end{array}\right..$

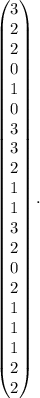
$\left(\begin{array}{}3&2&2&0&1\\0&3&3&2&1\\1&3&2&0&2\\ 1&1&1&2&2\end{array}\right).$

Поменяем местами 1-ю и 3-ю строки:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 1&1&1&2&2\end{array}\right).$

Вычитаем из 4-й строки 1-ю строку:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 0&-2&-1&2&0\end{array}\right).$

Вычитаем из 3-й строки 1-ю строку, умноженную на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Разделим 2-ю строку на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 3-ю и 2-ю строку, умноженную на 7:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 1-ю и 2-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 4-ю и 2-ю строку, умноженную на 2:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&0&1&\frac{10}{3} &\frac{2}{3} \end{array}\right).$

Поменяем местами 4-ю и 3-ю строки:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 3-ю и 1-ю строки:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 2-ю и 3-ю строку, умноженную на -1:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 4-ю и 3-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&-\frac{16}{3} &-\frac{14}{3} \end{array}\right).\\$

Разделим 4-ю строку на -16/3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

Суммируем 1-ю и 4-ю строку, умноженную на -4/3:

$\left(\begin{array}{}1&0&0&0 &\frac{1}{2} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

Суммируем 2-ю и 4-ю строку, умноженную на 8/3:

$\left(\begin{array}{}1&0&0&0 &\frac{1}{2} \\0&1&0&0 &2 \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

Суммируем 3-ю и 4-ю строку, умноженную на -10/3:

$\left(\begin{array}{}1&0&0&0 &\frac{1}{2} \\0&1&0&0 &2 \\0&0&1&0 &-\frac{9}{4} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

$x_1=\frac{1}{2}\\x_2=2 \\x_3=-\frac{9}{4} \\x_4=\frac{7}{8}.$

4,6(59 оценок)

Ответ:

dinok3

02.03.2022

Відповідь:

(Понятия «больше» и «меньше» наряду с понятием равенства возникли в связи со счетом предметов и необходимостью сравнивать различные величины. Понятиями неравенства пользовались уже древние греки. Архимед (III в. до н. э.), занимаясь вычислением длины окружности, установил, что «периметр всякого круга равен утроенному диаметру с избытком, который меньше седьмой части диаметра, но больше десяти семьдесят первых».

Ряд неравенств приводит в своем знаменитом трактате «Начала» Евклид. Он, например, доказывает, что среднее геометрическое двух положительных чисел не больше их среднего арифметического и не меньше их среднего гармонического

Однако все эти рассуждения проводили словесно, опираясь в большинстве случаев на геометрическую терминологию. Современные знаки неравенств появились лишь в XVII— XVIII вв. Знаки < и > ввел английский математик Т. Гарриот (1560—1621), знаки ? и ? французский математик П. Бугер (1698—1758).)

Пояснення:

4,5(20 оценок)

Это интересно:

Компьютеры-и-электроника

08.06.2020

Подробная инструкция: Как установить McAfee SiteAdvisor для Chrome...

Финансы-и-бизнес

10.05.2020

Как избежать ошибок в дейтрейдинге...

Хобби-и-рукоделие

18.12.2021

Как сделать кожаные браслеты своими руками: простые шаги для начинающих...