Возьмем две точки 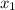 ,
, 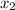 , причем
, причем 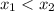 .
.
Им соответствуют значения функции 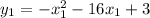 и
и 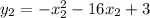 .
.
Сравним значения функций в данных точках. Для этого достаточно посмотреть на знак их разности 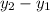 : если он положительный, то
: если он положительный, то 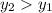 ; если равен нулю, то значения равны; иначе
; если равен нулю, то значения равны; иначе 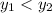 .
.
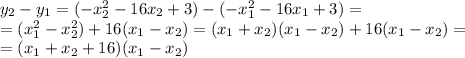
По предположению, 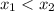 , поэтому вторая скобка отрицательна.
, поэтому вторая скобка отрицательна.
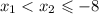 , то сумма
, то сумма 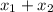 меньше -16, тогда первая скобка тоже отрицательна, а всё произведение положительно и
меньше -16, тогда первая скобка тоже отрицательна, а всё произведение положительно и 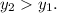 Получили, что большему значению аргумента соответствует большее значение функции, тогда на отрезке
Получили, что большему значению аргумента соответствует большее значение функции, тогда на отрезке ![(-\infty,-8]](/tpl/images/4748/4663/9ac1f.png) функция возрастает.Аналогично, для
функция возрастает.Аналогично, для 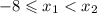 произведение отрицательно. Здесь большему значению аргумента соответствует меньшее значение значение функции, по определению это значит, что функция убывает.
произведение отрицательно. Здесь большему значению аргумента соответствует меньшее значение значение функции, по определению это значит, что функция убывает.
ответ: доказано
Объяснение:
если через производную, то она равна -2х-16, находим критическую точку -2х-16=0, х=8
с неравенства 2х-16≥0 устанавливаем знак производной при переходе через критическую точку
-8
+ -
значит, функция возрастает на промежутке (-∞;-8] и убывает на промежутке [-8;+∞)
Кстати, этот же результат получим, решив вторым .
вершина параболы имеет абсциссу х₀=-b/2a=16/(-2)=-8, т.к. ее ветви направлены вниз, то функция возрастает на промежутке (-∞;-8] и убывает на промежутке [-8;+∞)