ответ: ∈
∈ ![[-5 ; -\sqrt{3}]](/tpl/images/1008/3859/da582.png) ∪
∪ ![[\sqrt{3};5]](/tpl/images/1008/3859/34029.png)
Объяснение:
Область определения или область задания функции — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено.
Для 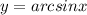
 ∈
∈![[-1 ; 1]](/tpl/images/1008/3859/dff6b.png)
Для 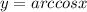
 ∈
∈![[-1 ; 1]](/tpl/images/1008/3859/dff6b.png)
Решаем систему:
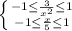
Четыре уравнения.
1) 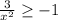 ⇒
⇒ 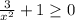
Выполняется для любых  .
.
2) 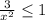 ⇒
⇒ 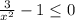 ⇒
⇒
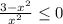
Дробь может быть меньше либо равно нулю тогда и только тогда, когда ее числитель неотрицателен, а знаменатель отрицателен, либо когда ее числитель отрицателен или равен нулю, а знаменатель положителен, т.е. в первом случае:
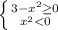
 ∈∅ (ни один
∈∅ (ни один  не удовлетворяет данному условию, так как
не удовлетворяет данному условию, так как 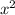 всегда положителен)
всегда положителен)
Во втором случае:
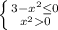 ⇒
⇒ 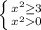 ⇒ решением этого случая будет являться:
⇒ решением этого случая будет являться:
 ∈
∈ ![(-\infty;-\sqrt{3}]](/tpl/images/1008/3859/aebdf.png) ∪
∪ 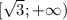
3) 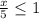 ⇒
⇒ 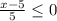 ⇒
⇒ 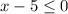 ⇒
⇒ 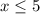
4) Аналогично третьему уравнению находим:
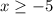
Находим пересечение всех полученных промежутков:
1) ∀
2)  ∈
∈ ![(-\infty;-\sqrt{3}]](/tpl/images/1008/3859/aebdf.png) ∪
∪ 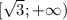
3) 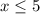
4) 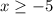
ответ:  ∈
∈ ![[-5 ; -\sqrt{3}]](/tpl/images/1008/3859/da582.png) ∪
∪ ![[\sqrt{3};5]](/tpl/images/1008/3859/34029.png)
найдите сумму бесконечной геометрической прогрессии -40; 20; -10; ...
член геометрической прогрессии определяется по формуле
вn=в1*q^(n-1),или в2=в1*q^(2-1)= в1*q¹=в1q
т.к. в1=-40; в2=20, по условию задачи, можно найти q, подставляем данные и находим
20=-40*q, q=-½
т.к не дано найти сумму ограниченного количества членов , то можно рассуждать так, суммы n членов определяется по формуле
Sn=в1*(1-q^n)/(1-q), т.к q=-½, тогда q^n=(-½)^n≈0 при n→∞, (-0,5;0,3;-0,25, т.е при увеличении n, q≈0, и этим членом можно пренебречь), тогда, подставив данные получим
Sn=-40*1/(1-(-½))=-40*2/3=-26⅔
либо 6x=0 либо (x-0.6)=0
x=0
x=0.6