1661
Объяснение:
По условию на доске написаны составные числа
a₁, a₂, ..., aₓ,
где aₓ ≤ 1700 и НОД(a₁, a₂)=...=НОД(a₁, aₓ)=НОД(a₂, a₃)=...=
=НОД(a₂, aₓ)=...=НОД(aₓ₋₁, aₓ) = 11.
Как известно, любое составное число А можно представить в виде разложения на простые множители
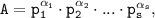
где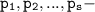 
простые числа, 
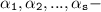неотрицательные целые числа.
Так как наибольший общий делитель (НОД) любых двух чисел равен 11, то разложение каждого числа содержит множитель pₓ = 11 и αₓ = 1, а остальные простые множители любой пары различны. Отсюда, первое число, которого написал Олег - это 11. Далее, последовательность можно представить в виде
11·2, 11·3, 11·5, 11·7, 11·11, ..., 11·pₐ.
Из 11·pₐ ≤ 1700 находим pₐ:
11·pₐ ≤ 1700
pₐ ≤ 1700:11
pₐ ≤ 154 6/11.
Наибольшее простое число удовлетворяющее последнее неравенство - это 151. Тогда 11·151= 1661.
x ≠ - 2; x ≠ 0
24x + x( x + 2) - 24(x+ 2) = 0
24x + x^2 + 2x - 24x - 48 = 0
x^2 + 2x - 48 = 0
D = 4 + 4*48 = 196 = 14^2
x1 = ( - 2 + 14)/2 = 12/2 = 6;
x2 = ( - 2 - 14)/2 = - 16/2 = - 8;
ответ:
- 8; 6