в детстве человек счастлив, как сейчас говорят, по умолчанию. по природе своей ребенок - существо, инстинктивно предрасположенное к счастью. какой бы трудной и даже трагичной ни была его жизнь, он все равно радуется и постоянно находит для этого все новые и новые поводы. возможно, потому, что ему пока не с чем сравнить свою жизнь, он еще не подозревает, что может быть как-то иначе. но, скорее всего, все-таки потому, что детская душа еще не успела покрыться защитным панцирем и более открыта добру и , чем душа взрослого человека.
а с возрастом все словно бы выворачивается наизнанку. как бы спокойно и благополучно ни складывалась наша жизнь, мы не успокоимся, пока не найдем в ней некую занозу, нескладицу, неполадку, прицепимся к ней, и почувствуем себя глубоко несчастными. и мы верим в придуманную нами драму, искренне жалуемся на нее друзьям, тратим на переживания время, здоровье, душевные силы… лишь когда случается действительно настоящая трагедия мы понимаем, сколь нелепы выдуманные страдания и сколь пустячен повод для них лишь тогда. тогда мы хватаемся за голову и говорим себе: «господи, каким же я был глупцом, когда так парился из-за какой-то ерунды. нет чтобы жить в своё удовольствие и наслаждаться каждой минутой.
это писала моя сестра давно ну и вот решила тут написать;)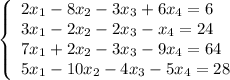
Для удобства вычислений, поменяем местами строчки системы ЛНУ .

1 строку * 7 - 5*2 строку ; 1стр*3 - 5*3стр ; 1стр*2-5*4стр
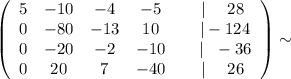
2стр - 4*3стр ; 3 стр + 4стр
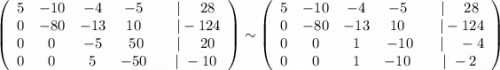
Для перехода к последней матрице разделили 3 строку на (-5) , а 4 строку на 5 .
Ранг матрицы системы ( та, что записана до вертикальной черты, размером 4×4 ), равен 3, так как две последние строки равны, а значит одну из строк можно вычеркнуть. Ранг расширенной матрицы ( та, что записана без учёта вертикальной черты, размером 4×5 ) равен 4, так как2 последние строки различны. Ранги указанных матриц НЕ равны, то есть условия теоремы Кронекера-Капелли не выполняются, значит система НЕ ИМЕЕТ РЕШЕНИЙ, то есть система НЕСОВМЕСТНА .
Общее решение системы можно было бы записать лишь в случае, если бы система была совместна и не определена .

пусть х - это расстояние, пройденное пешком, а 6х - расстояние на автобусе, тогда скорость пешком=х\4,5, скорость на автобусе - 6х\4,5*10, а время - 3 ч 12 мин=3,2 часа.
S=V*t; V=S:t Составим уравнение
1) х\4,5+6х\4,5*10=3,2 - приведем к общему знаменателю
10х\45+6х\45=3,2
16х:45=3,2
16х=3,2*45
16х=144
х=144:16
х=9 км пешком
2) 9*6=54 км - проехали на автобусе
3) 9+54=63 км - длина всего маршрута
Проверим: 9 км со скоростью 4,5 км\ч=2 часа, плюс 54 км со скоростью 45 км\ч=1,2 часа.Всего - 3,2 часа или 3 часа 12 минут.
ответ: длина туристического маршрута - 63 км.