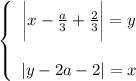
Область определения:
Так как модули неотрицательны, то x ≥ 0 и y ≥ 0
Возможны 4 варианта:
1)
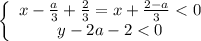
Тогда:
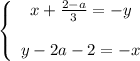
Переносим неизвестные налево, а числа с параметрами направо:
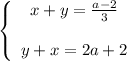
Слева части одинаковые. Если справа будут тоже одинаковые, то получится два одинаковых уравнения, то есть по сути одно.
Оно будет иметь бесконечно много решений, что нам и нужно.
(a - 2)/3 = 2a + 2
a - 2 = 6a + 6
5a = -8
a = -8/5 = -1,6
Подставляем в систему:
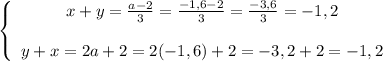
Из условия:
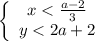
Получаем:
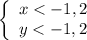
Но по области определений: x ≥ 0; y ≥ 0.
Получили противоречие, значит, в этом варианте решений нет.
2)
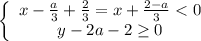
Тогда:
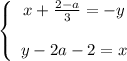
Переносим неизвестные налево, а числа с параметрами направо:
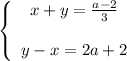
Складываем уравнения и получаем:
2y = (a-2)/3 + 2a + 2 = (a-2+6a+6)/3 = (7a+4)/3
Эта система всегда будет иметь одно решение.
y = (7a+4)/6
x = y - 2a - 2 = (7a+4)/6 - 2a - 2 = (7a+4-12a-12)/6 = -(5a+8)/6
Этот вариант нам не подходит.
3)
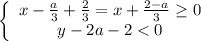
Тогда:
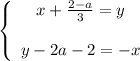
Переносим неизвестные налево, а числа с параметрами направо:
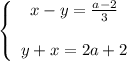
Складываем уравнения и получаем:
2x = (a-2)/3 + 2a + 2 = (a-2+6a+6)/3 = (7a+4)/3
Эта система всегда будет иметь одно решение.
x = (7a+4)/6
y = 2a + 2 - x = 2a + 2 - (7a+4)/6 = (12a+12-7a-4)/6 = (5a+8)/6
Этот вариант нам не подходит.
4)
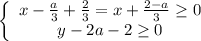
Тогда:
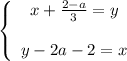
Переносим неизвестные налево, а числа с параметрами направо:
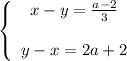
Или по-другому:
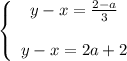
Слева части одинаковые. Если справа будут тоже одинаковые, то получится два одинаковых уравнения, то есть по сути одно.
Оно будет иметь бесконечно много решений, что нам и нужно.
(2 - a)/3 = 2a + 2
2 - a = 6a + 6
7a = -4
a = -4/7
Подставляем в систему:
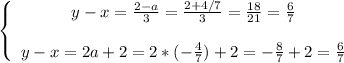
Из условия:
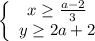
Получаем:
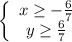
Но по области определения: x ≥ 0
При a = -4/7 будет:
x ∈ [0; +oo); y = x + 6/7 - бесконечно много решений.
Объяснение:
Разность в установке составляет:
8675 - 5000 = 3675 руб.
Экономия составляет 3,5 - 1,5 = 2 руб в час при пользовании 7 часов в сутки. То есть 2*7 = 14 часов в сутки.
Потому что стоимость дневного тарифа - одинакова у обоих счетчиков.
Через 3675/14 = 262,5 суток стоимость установки и обслуживания сравняется.
Через 263 суток он получит первые 0,5*14 = 7 рублей экономии.
Только эта таблица - неправильная.
На самом деле у двухтарифного счетчика стоимость дневного тарифа НАМНОГО выше, чем у однотарифного.
{a₁ +a₄=13;a₂+a₆=22.
---
a₆ -?
{a₁ +a₄=13;a₂+a₆=22.⇔{a₁ +a₁+3d=13; a₁+d+a₁+5d=22.⇔
{2a₁ + 3d=13; 2a₁+6d=22.⇒{3d =22-13 ;a₁ + 3d=11. {d =3 ;a₁ =2.
a₆ =a₁ + 5d =2+5*3 =17.
{a₃ +a₆=13 ;a₅ =8.
S₁₀ -?
{a₃ +a₆=13 ;a₅ =8.⇔{(a₁ + 2d) + (a₁ + 5d)=13; a₁+4d=8. ⇔
{2a₁ + 7d=13; a₁+4d=8.⇔{2a₁ + 7d=13; 2a₁+8d=16.⇒{d =16-13; a₁+4d=8.⇔
{d =3; a₁= -4.
S₁₀ =(2a₁ +9d)/2 *10 = 5(2a₁ +9d)=5(2*(-4) +9*3)= 5*19 =95.
Геометрическая прогрессия
{a₁ +a₄=13 ; a₄ + a₇ =13.
---
q -?
{a₁ +a₄=13 ; a₄ + a₇ =13.⇒a₇ - a₁ =13-13 ⇔a₁q⁶ - a₁ =0 ⇔ a₁(q⁶ - 1) =0.
ясно a₁≠0 , следовательно q⁶ - 1=0 ⇔(q³ -1)(q³ +1)=0⇒ [q³ =1 ; q³ =1.
q = 1. [ q = - 1 не удовлетворяет a₁ +a₄=13⇒a₁(1 +q³)=13]
* * * a₁(1 +q³)=13 ⇔2a₁=13 ⇒ a₁=a₂=a₃ =... =6,5. * * *
a₁ =81 ; q =1/3 ;a(n) =1.
---
S(n) - ? n -?
S(n) =(a₁ -a(n)q)/(1-q) =(81 -1*1/3)/(1-1/3) =242/2 =121.
a(n) =a₁ *q^(n-1) ;
1 =81*(1/3) ^(n-1) ;
1/81 =(1/3) ^(n-1) ;
(1/3)⁴ =(1/3) ^(n-1);
4 =n-1 ⇒ n =5 .