Объяснение:
Любое простое число нечетно и его квадрат запишем так
(2х+1)^2 = 4х^2+4х+1
т. е. при делении квадрата простого числа на 4 остаток 1
Любое простое число не делится на 3, значит можно записать или как кратное 3+1 или как кратное 3+2.
Квадрат такого числа будет выглядеть
(3х+1)^2 = 9х^2+6х+1
или
(3х+2)^2 = 9х^2+12х+4 =9х^2+12х+3+1
т. е при делении квадрата простого числа на 3 в обоих случаях остаток 1
В итоге квадрат простого числа можно записать как 4*3*у+1, что равно 12*у+1, что и требовалось, поделив его на 12 получим остаток 1
3. 2; 3 4. убывающей
Объяснение:
3. Корень извлекается только из неотрицательных чисел. Поэтому
![1-x^2\geq 0\\x^2\leq 1\\x\in[-1;1]](/tpl/images/1412/3606/2ee37.png)
Находим значения функции на границах отрезка
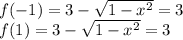
Находим точки в которых производная равна нулю.
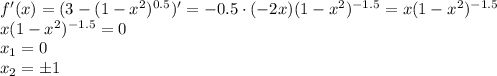
Второе значение уже нами исследовалось.
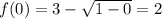
Следовательно
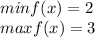
4. Функция f является возрастающей, т.е. чем больше аргумент, тем больше значение функции и наоборот, чем меньше аргумент, тем меньше значение функции.
Функция g(x) является убывающей т.к. это прямая, в уравнении которой коэффициент при х отрицательный.
Тогда в функции f(g(x)) аргументы будут убывать, следовательно, как было выяснено ранее, будут убывать и значения функции. Значит, функция будет убывающей.
а) log2 (x-3) + log2 (3x-2)= log2 6
x-3 > 0; x > 3
3x-2 > 0; x > 2/3
log2 (x-3)(3x-2) = log2 6
3x^2 - 2x + 9x + 6 = 6
3x^2 +7x = 0
x(3x+7) = 0
x = 0, x = -7/3
Корни не подходят под одз - значит нет решений
б) log5 (x^2+4)/(x-3) = log5 x
x > 0
(x^2+4)/(x-3) > 0; x - 3 > 0; х > 3
(x^2+4)/(x-3) = x
x^2 +4 = x^2 - 3x
-3x = 4
x = -4/3
снова нет решений
в) lg x^2=1
x^2 = 10
x = +- корень из 10