Объяснение:
1.
a) ОДЗ: x²-9≠0 (x+3)(x-3)≠0 x₁≠-3 x₂≠3.
б)
x²-2x-15≠0 D=64 √D=8
x₁≠-3 x₂≠5.
x²+8x+15≠0 D=4 √D=2
x₃≠-5 x₄≠-3. ⇒
ОДЗ: x₁≠-5 x₂≠-3 x₃≠5.
2.
a) (x²+4)/(x-1)=5x/(x-1) ОДЗ: x-1≠0 x≠1
x²+4=5x
x²-5x+4=0 D=9 √D=3
x₁=1 ∉ОДЗ х₂=4
ответ: х=4.
б)
(x+3)/x=(2x+10)/(x-3) ОДЗ: x₁≠0 x-3≠0 x₂≠3.
(x+3)*(x-3)=x*(2x+10)
x²-9=2x²+10x
x²+10x+9=0 D=64 √D=8
ответ: x₁=-1 x₂=-9.
3.
Пусть скорость течения реки - х. ⇒
70/(10+х)=30/(10-х)
70*(10-x)=30*(10+x)
700-70x=300+30x
100x=400 |÷100
x=4.
ответ: скорость течения реки 4 км/ч.
1.
1) По условию ВМ=MD=14 см , где ВМ - высота параллелограмма АВCD.
2) AM+MD=AD
8см + 14см = 22см - длина стороны AD.
3) S = AD · ВМ - площадь параллелограмма АВCD.
22см · 14см = 308 см²
ответ: 308 см²
2.
Дано:
S = 12см²
ВК⊥AD
ВК = 2см
BM⊥DC
ВМ =3 см.
P=?
Решение.
1) S = AD · ВК - площадь параллелограмма.
AD = S : ВК
AD = 12 : 2 = 6 см - одна сторона параллелограмма.
2) S = DC · ВM - площадь параллелограмма.
DC = S : ВM
DC = 12 : 3 = 4 см - вторая сторона параллелограмма.
3) Р = 2· (AD+DС) - периметр параллелограмма.
Р = 2 · (6 + 4) = 20 см
ответ: 20 см.
3.
Дано:
Ромб QRMN
∠QRM = 60°
QD⊥RM
RD = 6
S=?
Решение.
1) ΔQRD - прямоугольный треугольник.
∠RQD = 90°- 60° = 30°
2) Катет, лежащий против угла 30 градусов, равен половине гипотенузы.
RD = 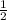 QR => QR = 2RD
QR => QR = 2RD
QR = 2 · 6 = 12см
QR=RM=MN=NQ - как стороны ромба.
3) По теореме Пифагора в прямоугольном треугольнике
RD²+DQ²=QR² => DQ²=QR² - RD²
DQ²=12² - 6²=144-36=108
DQ = √108 = 6√3 см - высота ромба
4) S = RM · DQ - площадь ромба
S = 12 · 6√3 = 72√3 ≈ 125
ответ: 72√3 см² или 125 см²