Объяснение:
Будет 2 случая:
1) Все числа равны 0, тогда их произведения равны 0 и выражение ab + bc + ca будет равно 0.
2) Числа равны произвольным действительным числам, в таком случае нужно рассмотреть равенство a + b + c = 0. Чтобы левая часть выражения была равна 0, необходимо, чтобы одно из чисел равнялось сумме двух других, поставленной с противоположным знаком. И далее если рассматривать выражение ab + bc + ca <= 0, с отрицательным знаком в любом случае будет 2 члена, в то время как третий будет со знаком плюс, и он будет меньше двух других, так как он получается из произведения Наименьших членов (они с одинаковым знаком, соответственно образуют +). Поэтому получится что ab + bc + ca будет меньше 0 в ЛЮБОМ СЛУЧАЕ.
Для примера можно взять числа 15, -7, -8 соответственно. В ab + bc + ca получится (-105) + (56) + (-120), что очевидно меньше 0.
8
Объяснение:
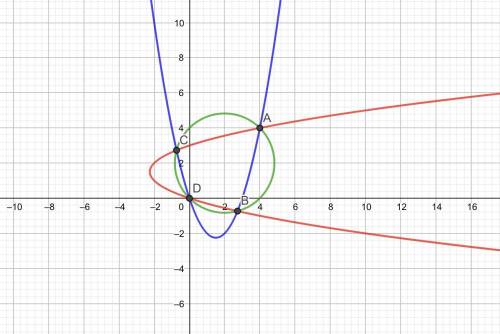
Складывая данные уравнения , получим : x² +y² = 4(x+y) ( 1 )
пусть x + y = a ⇒ y = a-x , подставим в ( 1 ) вместо y ( a -x ) :
x² +( a-x)² - 4a = 0 или : 2x² -2ax +a²-4a = 0 ( 2 )
уравнение (2) имеет решение , если D/4 ≥ 0 или :
a² -2(a² -4a) ≥ 0 ⇔ a² -8a ≤ 0 ⇔ 0 ≤ a ≤ 8 ⇒ наибольшее a , при
котором уравнение ( 2 ) имеет решение равно 8 ⇒ a ≤ 8 ;
проверкой убеждаемся , что пара ( 4 ; 4) является решением
системы и мы доказали , что x+y ≤ 8 ⇒ 8 - наибольшее
значение суммы (x+y)
78/26=3 часа ехал 1 мотоциклист
52*3=156 км проехал второй мотоциклист за 3 часа до встречи