Объяснение:
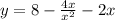
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
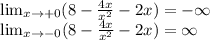
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
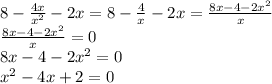
Решаем квадратное уравнение, находим точки пересечения с осью х:
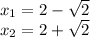
Находим точки экстремума (производная равна нулю).
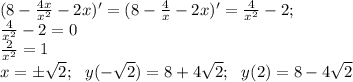
Для нахождения точек перегиба находим вторую производную
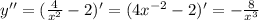
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
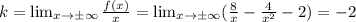
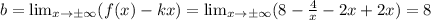
Наклонная асимптота есть:
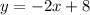
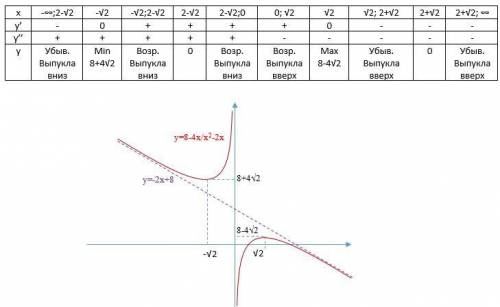
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
a) 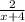
b) 
Объяснение:
Будем раскладывать на множиели при этой формулы :
ax² + bx +c = a(x - x₁)(x - x₂)
a) Для начала нам потребуется найти корни :
x² - x -20 = 0
{ x₁ + x₂ = 1 (система)
{ x₁ × x₂ = -20
x₁ = - 4
x₂ = 5
⇒ x² - x -20 = 1(x - (-4))(x - 5) = (x+4)(x-5)
Теперь подставляем это выражение в знаменатель, а также раскладываем на множители числитель :
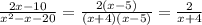
b) Так же, как и в примере, нам нужно найти корни, но уже двух многочленов : (x²+12x+27) и (x²+8x-9).
x² + 12x + 27 = 0
Буду решать через выделение полного квадрата :
(x + 6)² - 9 = 0
(x + 6)² = 9
x+6 = -3 x+6 = 3
x₁ = -9 x₂ = -3
⇒ x² + 12x + 27 = 1(x - (-9))(x - (-3)) = (x+9)(x+3)
Теперь разложим многочлен на множители, который в знаменателе :
x² + 8x - 9 = 0
Решаю опять же через выделение полного квадрата :
(x + 4)² - 25 = 0
(x + 4)² = 25
x+4 = -5 x+4 = 5
x₁ = -9 x₂ = 1
⇒ x² + 8x - 9 = 1(x - (-9))(x - 1) = (x+9)(x-1)
Теперь подставляем эти два выражения :
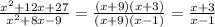
144x^2-66+74-8x^2=480
136x^2-472=0 разделим на 8
17x^2-59=0
17x^2=59
x^2=3,5
x1=-√3,5
x2=√3,5
ответ:-√3,5;√3,5
как-то так