В решении.
Объяснение:
а) Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
(2х² - 2)² - 4х³(х³ + х² - х - 2) + 4(х²)³ + 20х⁹/5х⁴ - 2(4х³ + 1) =
= 4х⁴ - 8х² + 4 - 4х⁶ - 4х⁵ + 4х⁴ + 8х³ + 4х⁶ + 4х⁵ - 8х³ - 2 =
= 8х⁴ - 8х² + 2. Стандартный вид. Степень (х⁴) = 4.
б) Докажите, что при любых целых значениях x многочлен делится на 2.
Так как коэффициенты при х чётные (8 и 8) и число 2 также чётное, при любых значениях х многочлен делится на 2.
в) Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
Так как 8х⁴ > 8х² и степени при х чётные, то есть, сами одночлены в составе многочлена не могут быть отрицательными, при любых действительных значениях x многочлен не может принимать отрицательных значений.
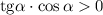
Если произведение двух выражений положительно, то либо каждое из этих выражений положительно, либо каждое из этих выражений отрицательно.
1. Каждое из этих выражений положительно:
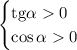
Тангенс положителен в 1 и 3 четверти, а косинус положителен в 1 и 4 четверти. Значит, указанное условие выполняется только в 1 четверти.
2. Каждое из этих выражений отрицательно:
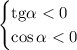
Тангенс отрицателен во 2 и 4 четверти, а косинус отрицателен во 2 и 3 четверти. Значит, указанное условие выполняется только во 2 четверти.
Таким образом, получаем, что угол 
может принадлежать 1 или 2 четверти.
ответ: 1 или 2
и синус и косинус - циклические функции с периодом в 360 градусов, поэтому пример можно привести к виду
4sin810+3cos720-3sin630+5cos900 = 4*sin(360+360+90)+3*cos(360+360)-3sin(360+270)+5*cos(360+360+180) = 4*sin(90)+3*cos(360)-3*sin(270)+5*cos(180) =
Все эти значения можно увидеть в таблице значений тригонометрических функций. Таким образом
= 4*1+3*1-3*(-1)+5*(-1) = 4+3+3-5 = 5.