На весь путь было затрачено 14 часов
Объяснение:
пусть х - скорость на 1-й половине пути.
х + 10 - скорость на 2-й половине пути
Половина пути составляет 840 км : 2 = 420 км
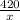 - время, затраченное на 1-ую половину пути
- время, затраченное на 1-ую половину пути
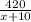 - время, затраченное на 2-ую половину пути
- время, затраченное на 2-ую половину пути
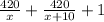 - время, которое было затрачено на весь путь
- время, которое было затрачено на весь путь
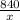 - время, которое планировалось затратить на весь путь
- время, которое планировалось затратить на весь путь
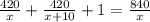
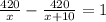
420(x + 10) - 420x = x² + 10x
x² + 10x = 420x + 4200 - 420x
x² + 10x - 4200 = 0
D = 10² + 4 · 4200 = 16 900
√D = 130
x₁ = 0.5(-10 - 130) = -70 (км/ч) - не подходит по физическому смыслу
x₂ = 0.5(-10 + 130) = 60 (км/ч) - скорость на 1-й половине пути
60 + 10 = 70 (км/ч) - скорость на 2-й половине пути
420 км : 60км/ч = 7ч - затрачено на 1-ю половину пути
420км : 70 км/ч = 6ч - затрачено на 2-ю половину пути
7ч + 6ч + 1ч = 14ч -затрачено на весь путь
 км/мин.
км/мин.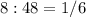 км/мин.
км/мин.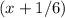 км/мин.
км/мин.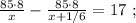
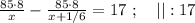
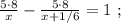
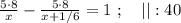
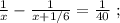
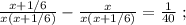
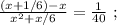
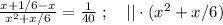
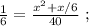
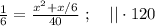
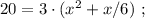
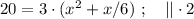
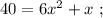
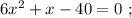
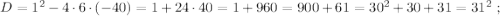
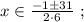
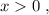 так, как это скорость,
так, как это скорость,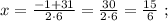
14 часов занял весь путь, включая время на остановку
Объяснение:
Пройдённый путь S зависит от скорости υ и времени t по формуле
S = υ · t или t = S / υ.
Пусть половину пути автомашина проехала со скоростью υ км/час. Тогда время t₀, потраченное на половину пути, равна
По условию, на оставшийся путь автомашина потратила на час меньше за счет увеличения скорости на 10 км/час, то есть проехала (t₀-1) час со скоростью (υ +10) км/час. Поэтому
Приравнивая скорость, получим:
42·(t₀-1)=42·t₀-t₀·(t₀-1)
t₀²-t₀-42=0
D=(-1)²-4·1·(-42)=1+168=169=13²
t₀=(1-13)/2=-6 - не подходит, так как время не отрицательно.
t₀=(1+13)/2=7 часов на половину пути. Тогда на весь путь
2·7=14 часов.