нехай перший рухався зі швидкістю х км/год, а другий у км/год. тоді перший пройшов до зустрічі 3х км, а другий 3у км., а разом 3х+3у=27 км за умовою перший прийшов на 1 год 21 хв=1,35 год раніше. тому 27/у-27/х=1,35 складемо систему рівнянь [latex] \left \{ {3x+3y=27} \atop {27/y-27/x=1.35}} \right. [/latex] виразимо в першому рівнянні х через у х=9-у підставимо в друге рівняння 20х-20у=ху . маємо: 180-20у-20у=9у-у² у²-49у+180=0 d=1681 y1=(49+41)/2=45 y2=4 тоді x1=9-45=-36 , що не задов умові і х2=9-4=5 км/год швидкість першого пішохода 5 км/год, а другого 4 км/год
рассмотрим наше уравнение:
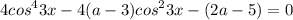
выполним замену cos²3x=t; t≥0
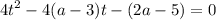
чтобы уравнение имело хотя бы один корень надо чтобы D≥0
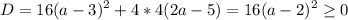
Это неравенство выполняется для любых a
тогда проверим корни, необходимо чтобы t≥0
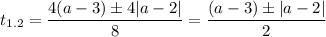
рассмотрим первый корень
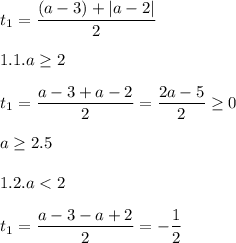
значит при а≥2.5 мы получим один положительный корень (относительно t)
проверим второй корень
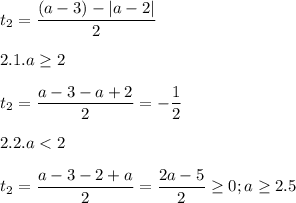
тут положительных корней не получим.
значит рассмотрим один положительный корень t=(2a-5)/2. при а≥2,5
выполним обратную замену
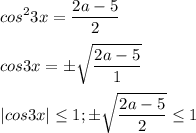
рассмотрим положительный корень
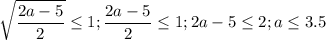
рассмотрим отрицательный корень
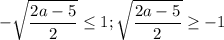
выполняется для всех а≥2.5
Собираем все вместе 2,5≤а≤3,5
равно =0 решение писать день)