2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
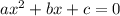
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
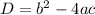
Формула корней:
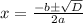
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
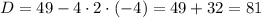
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
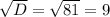
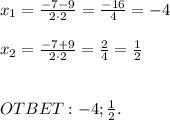
Нам нужно найти корни квадратного уравнения 9x2 - 7x - 2 = 0. И начнем мы традиционно с вычисления дискриминанта уравнения.
Для этого мы вспомним формулу:
D = b2 - 4ac, а так же выпишем коэффициенты, которые мы должны подставить в формулу:
a = 9; b = -7; c = -2.
Итак, подставляем значения и вычисляем:
D = (-7)2 - 4 * 9 * (-2) = 49 + 72 = 121;
Мы получили положительный дискриминант и можем говорить о том, что уравнение имеет два корня:
x1 = (7 + √121)/2 * 9 = (7 + 11)/18 = 18/18 = 1;
x2 = (7 - √121)/2 * 9 = (7 - 11)/18 = -4/18 = -2/9.
а)х2 - 6х < 0
х2 - 6х = 0
х(х - 6) = 0
1) х = 0
2)х - 6 = 0
х = 6
Нанеси на интервалы. В первом интервале будет плюс, во втором минус, в третьем плюс. Точки выколотые (незакрашенные), значит ответ: (0;6)