![\log_{8}{4-2x} \geq 2 \\ 4-2x\ \textgreater \ 0 \\ -2x\ \textgreater \ -4 |*-1 \\ 2x\ \textless \ 4 |:2 \\ x\ \textless \ 2 \\ x $\in$ (-\infty;2) \\ 4-2x \geq 64 \\ -2x \geq 60 |:-2 \\ x \leq -30 \\ x $\in$(\infty; -30]](/tpl/images/0503/1127/3f89d.png)
Для бинома
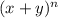
справедливы следующие утверждения:
1. Степени x начинаются со степени бинома n и уменьшаются до 0; степени y начинаются с 0 и увеличиваются до n. Последний член не имеет множителя x. Первый член не имеет множителя y, т.е.
2. Коэффициенты начинаются с 1 и увеличиваются на определенные значения (до среднего члена), а потом уменьшаются на те же значения обратно к 1.
3. Бином содержит n+1 членов
4. k-ый член можно найти следующим образом:
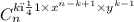
5. Средний член в биноме чётной степени находится по формуле:
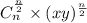
На основе теории решим данную задачу:
a) 4 + 1 = 5
b) 3. коэффициент этого члена выглядит так:
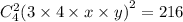
с) Из предыдущего пункта:
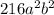
Примечание: Коэффициент при члене ab³ для данного бинома также равен 216