Сторона данного треугольника а(3) равна Р:3=6√3:3=2√3 дм
Формула радиуса окружности, описанной около правильного треугольника:
R=a/√3 =>
R=2√3:√3=2 дм
Формула стороны правильного многоугольника через радиус вписанной окружности:
а(n)=2r•tg(180°:n), где r – радиус вписанной окружности, n – число сторон,
Для правильного шестиугольника tg(180°:n)=tg30°=1/√3
a₆=2•2•1/√3=4/√3
P=6•4/√3=8√3 дм
—————
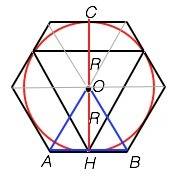
Как вариант: Правильный шестиугольник состоит из 6 равных правильных треугольников.
На рисунке приложения ОН - радиус описанной около правильного треугольника окружности и в то же время высота одного из 6 правильных треугольников, все углы которого 60°; АВ - сторона шестиугольника. Задача решается с т.Пифагора.
Часы на камине начали бить ровно в х ч 00 мин 00 сек.
Между ударами 4 сек. И закончили в x ч 00 мин (4x-4) сек.
12 ударов пройдут в такие моменты:
x:00:00; x:00:04; x:00:08; x:00:12; x:00:16; x:00:20; x:00:24;
x:00:28; x:00:32; x:00:36; x:00:40; x:00:44
Часы на башне начали бить в x ч 00 мин 02 сек.
Между ударами 3 сек. И закончили в x ч 00 мин (3x-1) сек
12 ударов пройдут в такие моменты:
x:00:02; x:00:05; x:00:08; x:00:11; x:00:14; x:00:17; x:00:20;
x:00:23; x:00:26; x:00:29; x:00:32; x:00:35
Теперь выпишем все подряд удары по времени:
x:00:00; x:00:02; x:00:04; x:00:05; x:00:08 (совпали); x:00:11;
x:00:12; x:00:14; x:00:16; x:00:17; x:00:20 (совпали); x:00:23;
x:00:24; x:00:26; x:00:28; x:00:29; x:00:32 (совпали); x:00:35
x:00:36; x:00:40; x:00:44.
Значит, удары совпали 3 раза, и получилось
x + x - 3 = 19 ударов
x = 11