и 
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при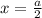 
.
Пусть сначала
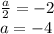
Тогда уравнение принимает вид 
и, очевидно, не имеет решений.
Пусть теперь
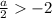
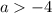
Если 
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
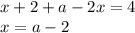
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если 
удовлетворяет системе неравенств
Решение системы: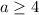 
Если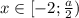 
, то уравнение принимает вид
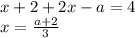
Полученный x будет корнем уравнения, если удовлетворяет системе:
Решение системы: 
Пусть, наконец,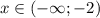 
. Тогда уравнение принимает вид
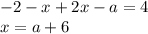
Полученный x будет корнем уравнения, если удовлетворяет системе:
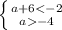
Эта система не имеет решений.
Теперь пусть 
, то есть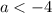 
.
Если 
, то
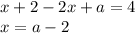
Система:
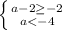
Нет решений.
Если 
, то
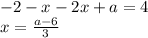
Система:
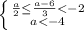
Решение системы: 
И наконец, если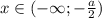 
, то
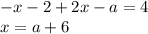
Система:
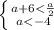
Решение: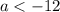 
Из вышесказанного очевидно, что
При 
- два решения
При - одно решение
При 
- нет решений
При 
- нет решений
При - одно решение
При 
- два решения
Таким образом, уравнение имеет одно решение при и
и
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при .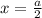
Пусть сначала
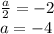
Тогда уравнение принимает вид и, очевидно, не имеет решений.
Пусть теперь
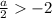
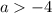
Если , то оба модуля раскрываются с плюсом и уравнение принимает вид:
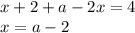
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если удовлетворяет системе неравенств
Решение системы: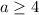
Если 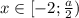, то уравнение принимает вид
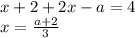
Полученный x будет корнем уравнения, если удовлетворяет системе:
Решение системы:
Пусть, наконец, 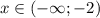. Тогда уравнение принимает вид
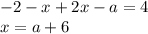
Полученный x будет корнем уравнения, если удовлетворяет системе:
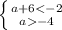
Эта система не имеет решений.
Теперь пусть , то есть .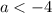
Если , то
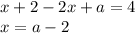
Система:
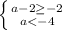
Нет решений.
Если , то
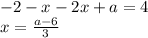
Система:
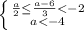
Решение системы:
И наконец, если 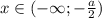, то
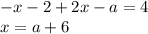
Система:
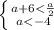
Решение: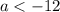
Из вышесказанного очевидно, что
При - два решения
При - одно решение
При - нет решений
При - нет решений
При - одно решение
При - два решения
Таким образом, уравнение имеет одно решение при и
Функция у нас дробная. Известно, что дробь принимает наибольшее значение тогда, когда знаменатель принимает своё наименьшее значение. Что у нас в знаменателе? Правильно, квадратичная функция y=x^2-6x+13,графиком которой является парабола, ветви которой направлены вверх ( a>0). Такая парабола принимает только наименьшее значение в своей вершине.Наибольшего значения она не имеет. Х вершина = -b/2a=6/2=3. Итак, свое наименьшее значение парабола принимает в точке х=3.
Подставим "3" в формулу параболы и найдем значение У вершины( или,иными словами,значение знаменателя):
3^2-6*3+13=4.
Итак, 8/4=2 и получается, что "2" - наибольшее значение функции Y=8/(x^2-6x+13).
Теперь докажем, что на промежутке [3;+ беск.) функция убывает:
функция монотонно убывает на промежутке [3;+ беск.), если для любых точек х1 и х2 из этого промежутка выполняется следующее:
x1<x2 => f(x1)>f(x2).
Например, х1=3; x2=4 ( 3<4)
y(3)=[8/(9-18+13)] =2
y(4)= [8/(16-24+13)]=1,6
Итак, как видно 3<4=> y(3)>y(4) => функция монотонно убывает.