ответ: Если a-b= 7 a^7-b^7 всегда делится на 7 , но не всегда делится на 8 . ( Тем не менее существуют такие a и b при которых оно делится на 8)
Объяснение:
a^7 -b^7 автоматически делится на 8 , если числа a и b четны .
Поскольку тогда a^7 делится как минимум на 2^7 и b^7 делится как минимум на 2^7 , то есть a^7-b^7 делится на 2^7 , а значит делится и на 2^3 = 8
Приведем пример таких четных a и b разность которых делится на 7 :
a=20 ; b=6
a-b= 14= 7*2
Но однако это не значит , что если a-b делится на 7 , то
a^7-b^7 обязательно делится на 8 .
Пусть a=8 ; b=1
a-b=7
a^7-b^7 = 8^7 -1^7 =8^7 - 1 - очевидно что не делится на 8.
Предположительно у вас ошибка в переписывании условия.
Думаю надо узнать делится ли a^7-b^7 на 7 . В этом случае ответ да .
Пусть : a-b=7*n (n- целое число )
a= (7n+b)^7
a^7-b^7 = (7n+b)^7 -b^7
Не раскрывая скобок в выражении (7n+b)^7 понято , что все его одночлены кроме b^7 будут помножены на 7 . Таким образом сумма всех его членов кроме b^7 делится на 7 .
(7n+b)^7 =7*a+b^7 , где a - целое число
a^7-b^7 = (7n+b)^7 -b^7 = 7*a+b^7 -b^7 =7*a
Таким образом :
a^7-b^7 делится на 7.
Объяснение:
Пример №1.
Для решения данного уравнения надо вспомнить 6 свойство числовых неравенств, которое изучается по алгебре в 8 классе:
если произведение чисел равно нулю, то это значит, что один из множителей равен нулю.
То есть, мы приравниваем все скобки к нулю.
Приравниваем:
2x - 3 = 0
x + 1 = 0
3 - x = 0
Решаем линейные уравнения(Перенос чисел без переменной вправо с изменением знака на противоположный, а также деление на коэффициент при переменной).
x = 1`,5
x = -1
x = 3
Пример №2.
Уравнение, у которого первый коэффициент имеет четвертую степень, называется биквадратным.
Пусть x^2 - это t, а t положительно.
Тогда получим уравнение:
t^2 + 3t = 0
Решим квадратное уравнение: для этого t вынесем за скобку.
Получим:
t(t + 3) = 0
Если произведение двух чисел равно нулю, то один из множителей также равен нулю.
t = 0
t + 3 = 0
Откуда t = 0; t = -3
Но t - это икс в квадрате. То есть, нам надо извлечь корень квадратный из полученных результатов.
x^2 =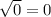 
x^2 =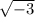 
- по условию не подходит, т.к. корень квадратный извлекать из чисел, меньших нуля, нельзя.
Задача решена. Если есть вопросы - задавай.
