Все таки не удержусь и для начала покажу красивый без метода мат индукции, а потом уже с методом мат. индукции.
Первый .(собственно то, как, возможно, была выведена эта формула)
Обозначим сумму ряда за S:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+n(n+1)!/2^n = S
Рассмотрим также вс сумму S1:
2!/2 +3!/2^2 + 4!/2^3 +...+(n+1)!/2^n = S1
Тогда не трудно убедится, что
S+2S1 = 3*2!/2 + 4*3!/2^2 + 5*4!/2^3+...+(n+2)(n+1)!/2^n =
= 3!/2 + 4!/2^2+ 5!/2^3+...+(n+2)!/2^n = 2*( 3!/2^2 + 4!/2^3 +...+(n+2)!/2^(n+1) =
= 2(S1 -2!/2 + (n+2)!/2^(n+1))
То есть получаем равенство:
S+2S1 = 2S1 -2! + (n+2)!/2^n
Замечаем, что 2S1 сокращается:
S = (n+2)!/2^n - 2
Что и требовалось доказать.
Второй (метод математической индукции)
Проверим, что тождество верно для n = 1:
1*2!/2 = 3!/2 - 2
1 = 3 - 2 - верно.
Предположим, что утверждение справедливо для n = t, то есть:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t = (t+2)!/2^t - 2
Докажем его справедливость для n = t+1
То есть нужно доказать, что:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t + (t+1)(t+2)!/2^(t+1) = (t+3)!/2^(t+1) - 2
Нетрудно заметить, что:
1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t + (t+1)(t+2)!/2^(t+1) =
= (1*2!/2 + 2*3!/2^2 + 3*4!/2^3+...+t(t+1)!/2^t) + (t+1)(t+2)!/2^(t+1) =
= (t+2)!/2^t - 2 + (t+1)(t+2)!/2^(t+1) = 2(t+2)!/2^(t+1) + (t+1)(t+2)!/2^(t+1) - 2 =
= (2+t+1)*(t+2)!/2^(t+1) - 2 = (t+3)((t+2)!/2^(t+1) - 2 = (t+3)!/2^(t+1) - 2
А значит, по принципу математической индукции, данное тождество доказано.
Можно доказать несколькими По т. Фалеса: Если параллельные прямые отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на второй стороне угла.
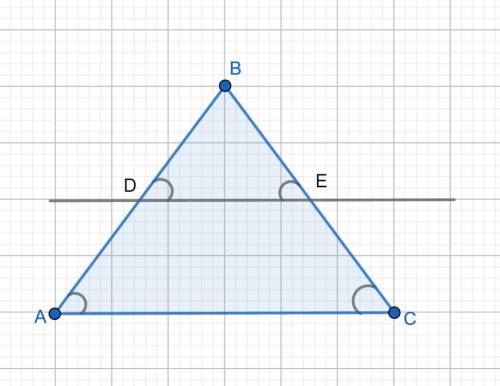
Параллельные прямые DE и AC отсекают равные отрезки на стороне AB угла ABC, т.е. AD = DB. Значит на стороне BC они отсекают также равные отрезки BE = EC.
2) Из подобия треугольников. Так как DE ║ AC, то ΔABC подобен ΔDBE по двум углам: ∠B общий, ∠BDE = ∠BAC как соответствующие при DE ║ AC и секущей AB. Так как по условию AD = DB, то BD/AB = 1/2. Коэффициент подобия k = 1/2. ⇒ BE/BC = 1/2, ⇒ BC = 2*BE, тч. E является серединой отрезка ВС.
3) Проведем прямые BO ║AC и ON║AB.
DBON параллелограмм, так как его противолежащие стороны параллельны. ⇒ DB = EO. ADEN параллелограмм, так как его противолежащие стороны параллельны, так как AD=DB, то NE=EO.
ΔBEO = ΔNEC по второму признаку: ∠BEO = NEC вертикальные, ∠BOE = ∠ENC внутренние накрест лежащие при BO ║AC и секущей ON. OE = EN. Из равенства треугольников следует BE=EC. ( так доказывается т. Фалеса)
x= - 35:4
x= - 8,75
(-8,75+5)*7 - 2*(-8,75) +8,75= -3,75*7 + 17,5 + 8,75= - 26,25 +26,25=0