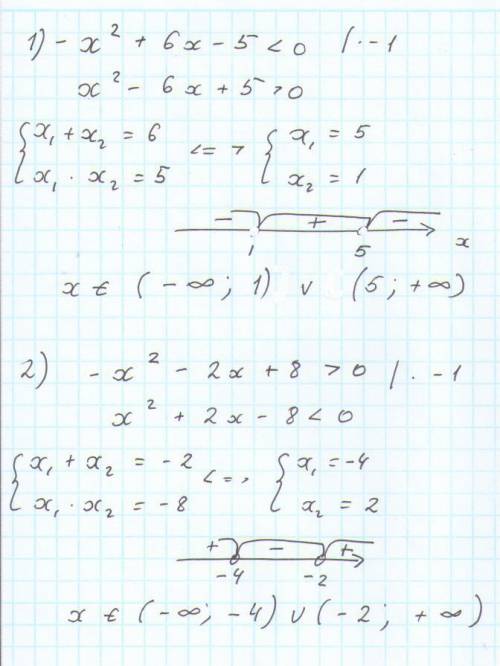
Чтоб найти числовое значение многочлена a2+2ay+y2 при a=8 и y=−7, нужно в выражение подставить известные значения а и у, и решить его.
а2 + 2ау + у2 = (8)2 + 2 * 8 * (- 7) + (- 7)2;
Возносим (8) и (- 7) квадрату:
(8)2 = 64;
(- 7)2 = 49;
Умножаем:
2 * 8 * (- 7) = 16 * (- 7) = - 112;
Подставляем значения в выражение:
64 + (- 112) + 49;
Раскрываем скобки:
64 - 112 + 49;
Вычитаем:
64 - 112 + 49 = - 48 + 49;
Добавляем:
- 48 + 49 = 1.
ответ: числовое значение многочлена a2+2ay+y2 при a=8, y=−7 равен 1
Пусть 1 - это длина всего пути
х км/ч - скорость первого автомобиля (ОДЗ: x>0)
1/х час - время, затраченное на весь путь первым автомобилем
1/2 : 30 = 1/60 час - время, затраченное на первую половину пути вторым автомобилем
1/2 : (х+9) = 1/(2х+18) час - время, затраченное на вторую половину пути вторым автомобилем
По условию время, затраченное на весь путь первым автомобилем равно времени, затраченному на весь путь вторым автомобилем, получаем уравнение:
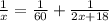
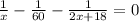
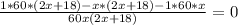
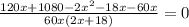
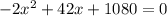
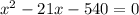
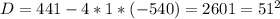
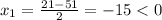
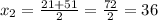км/ч - скорость первого автомобиля
ответ: 36 км/ч
