Производительность двух рабочих вместе:
v = 100 (дет./ч)
Производительность второго рабочего:
v₂ = 120/t (дет./ч)
Производительность первого рабочего:
v₁ = 120/(t + 1) (дет./ч)
Тогда: vt = v₁t + v₂t
100t = 120 + 120t/(t + 1)
100t(t + 1) = 120(t + 1) + 120t
100t² + 100t - 120t - 120 - 120t = 0
5t² - 7t - 6 = 0 D = b²-4ac = 49+120 = 169
t₁ = (-b+√D)/2a = (7+13):10 = 2 (ч)
t₂ = (-b -√D)/2a = -0,6 - не удовл. условию
Таким образом, скорость работы второго рабочего:
v₂ = 120:2 = 60 (дет./ч)
И на изготовление 300 деталей ему понадобится время:
t₂' = 300 : 60 = 5 (ч)
ответ: за 5 часов.
Геометрическая прогрессия:
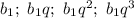
По условию все члены - натуральные числа, значит 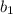 и
и 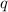 - натуральные
- натуральные
Найдем сумму первых 4 членов по формуле:
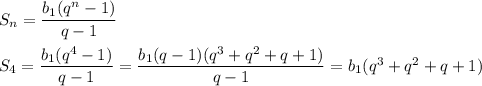
По условию эта сумма равна 80:
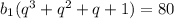
Преобразуем левую часть:
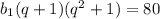
Предположим, что 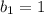 . Тогда:
. Тогда:
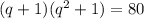
Рассмотрим в качестве второго сомножителя 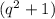 числа - делители числа 80.
числа - делители числа 80.
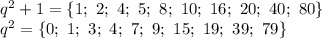
Имеется всего четыре точных квадрата:
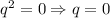 - не геометрическая прогрессия.
- не геометрическая прогрессия.
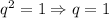 (отрицательные значения не рассматриваем) - все члены прогрессии равны 1, их сумма равна 4 - не подходит.
(отрицательные значения не рассматриваем) - все члены прогрессии равны 1, их сумма равна 4 - не подходит.
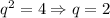 - члены прогрессии равны 1, 2, 4, 8 в сумме дают 15 - не подходит.
- члены прогрессии равны 1, 2, 4, 8 в сумме дают 15 - не подходит.
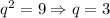 - члены прогрессии равны 1, 3, 9, 27 в сумме дают 40 - не подходит.
- члены прогрессии равны 1, 3, 9, 27 в сумме дают 40 - не подходит.
При рассмотрении других значений  , состав делителей числа
, состав делителей числа 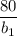 будет уменьшаться, однако никаких новых чисел, отличных от ранее выписанных не будет.
будет уменьшаться, однако никаких новых чисел, отличных от ранее выписанных не будет.
Таким образом, остается определить может ли при каком-либо значении 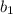 знаменатель равняться 1, 2 и 3.
знаменатель равняться 1, 2 и 3.
Если 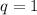 , то последовательность постоянная. Очевидно. что каждый член такой прогрессии (если такие прогрессии допускаются по условию) равен
, то последовательность постоянная. Очевидно. что каждый член такой прогрессии (если такие прогрессии допускаются по условию) равен 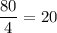 . Наибольший член в таком случае равен 20.
. Наибольший член в таком случае равен 20.
Если 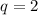 , то рассмотрим формулу для суммы:
, то рассмотрим формулу для суммы:
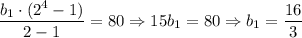
16/3 - не натуральное число, такой случай не удовлетворяет условию
Если 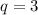 , то также рассмотрим формулу для суммы:
, то также рассмотрим формулу для суммы:
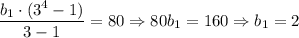
Следовательно, члены прогрессии 2, 6, 18, 54. Наибольший - 54.
Прогрессия 20, 20, 20, 20 с максимальным элементом 20 (если учитывать рассмотрение постоянных прогрессий со знаменателем 1, потому что слово "наибольший", возможно, предполагает то, что все члены последовательности должны быть различны).
Прогрессия 2, 6, 18, 54 с максимальным элементом 54.
Делим гири на три равные по весу кучки по следующему принципу:
Т.е. мы выстраиваем гири в порядке возрастания и разбиваем их на сегменты по шесть штук. Из каждого такого сегмента мы выбираем по две гири: 1-ю и 6-ю в первую кучку, 2-ю и 5-ю во вторую кучку, 3-ю и 4-ю в третью. Кучки будут содержать равное количество гирь (т.к. 552 делится нацело на шесть). Нам осталось убедиться, что они будут равными и по весу. [Вообще, это очевидно. Вес гирь, которые мы кладём в ту или иную кучку на каждом шаге одинаков (на первом – каждая пополняется на 7 г., на втором – на 19 г., на n-ом – на 12n - 5 г.)]. Для этого воспользуемся формулой суммы арифметической прогрессии (как нетрудно заметить, вес каждой кучки представим в виде суммы двух арифметических прогрессий).
Вес первой кучки:
Вес второй кучки:
Учитывая, что вес всех гирь:
считать вес третьей кучки не обязательно. Он по необходимости будет равен 50876.