Объяснение:
x²-19x+g=0 , x1=x , x2=x1+3
(podstawlajem)
{x1² - 19x1+g=0
{(x1+3)²-19*(x1+3)+g=0
{x1²-19x1+g=0
{x1²+6x1+9-19x1-57+g=0
{x1²-19x1+g=0
{x1²-13x1-48+g=0
{x1²-19x1+g=0
{x1²-13x1+g=48 * (-1)
{ x1²-19x1+g=0
(+) {-x1²+13x1-g=-48 (składywajem)
-6x1=-48
x1=8
(podstawlajem x1=8 do (1) urawnienija x²-19x+g=0
8²-19*8+g=0
64-152+g=0
g=88
kwdratowe urawnienije ma postać: x²-19x+88=0
po formule VIETA liczymy wtoroj korień x2
x1*x2=g
8*x2=88 // : 8
x2=11
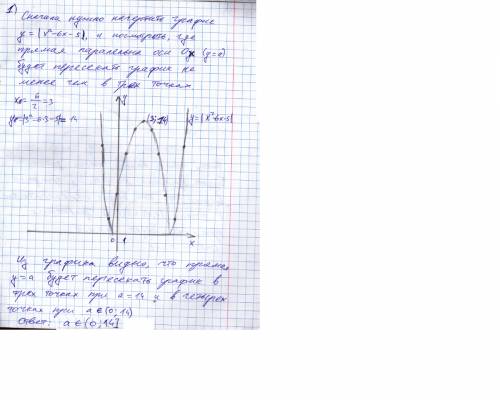
1) квадратное уравнение с модулем будет иметь не менее трех корней если прямая а проходит через вершину параболы -(x^2-6x-5) - это верхнее значение параметра,
а нижнее а=0.
находим вершину параболы, х0=-b/2a у нам b=6 a=-1 x0=3
y0=-9+5+18=14
значит а [0;14]
2) sqrt(x-1)=a+x x>=1
x-1=x^2+a^2+2ax
x^2+(2a-1)x+a^2+1=0
D>0 (2a-1)^2-4a^2-4>0 -4a-3>0 a<-3/4
3) 4x^2-15x+4a^3=0
x1=x2^2
x1*x2=a^3
x2^3=a^3 x2=a
15/4=x1+x2 15/4=a^2+a
4a^2+4a-15=0 a1=3/2 a2=-5/2
x^2-ax+(a-1)=0
x1^2+x2^2=(x1+x2)^2-2x1x2=17
a^2-2(a-1)=17
a^2-2a-15=0
a1=5 a2=-3