Объяснение:
Собственная скорость Vc= х км/ч.
Против течения :
t₁ = S/(Vc- Vт) = 18 / (x-3) (ч.)
По течению:
t₂= S/ (Vc+Vт) = 48/ (x+3) (ч.)
Всего:
t₁+t₂=3 (ч.)
18/(х-3) + 48/(х+3) = 3 |× (x-3)(x+3)
18(x+3) + 48(x-3) = 3(x-3)(x+3)
18x+54 + 48x - 144= 3(x²-9)
66x -90 = 3x² - 27 |÷3
22x - 30 = x²-9
x²-9 -22x+30=0
x²-22x+21=0
D= (-22)² -4*1*21 = 484-84=400 ; √D= 20
x₁= (22 -20) /2 =2/2=1 - не удовл. условию, т.к. скорость лодки не может быть меньше течения реки
x₂= (22+20)/2= 42/2=21 (км/ч) Vc
ответ: Vc= 21 км/ч.
В обоих случаях нужно делать замену переменной.
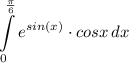
Что тут можно предпринять? Известно,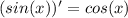 
, вот и сделаем замену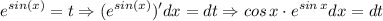 
Вообще идеально, получим простейший интеграл. Так как это определенный интеграл, то обратную замену можно не делать, а просто пересчитать пределы по самой замененной функции
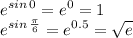
То есть пределы станут: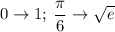 
А теперь сам интеграл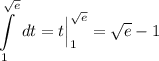 
Теперь следующий интеграл:
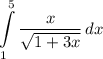
Что можно такого заменить? Попробуем взять корень, его производная даст тот же корень в знаменателе, да и сам 
вполне нормально выражается, делаем:
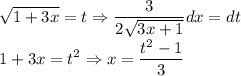
Заодно сразу новые пределы посчитаем:
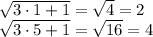
То есть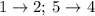 
Теперь подставляем и смотрим, что получается:
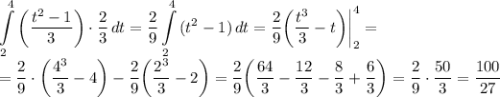
Можно, конечно, было и получить неопределенный интеграл и в него подставить старые пределы, но пересчет на новые позволяет не совершать часть действий
