√(7-x) + √(3x-5)=4
√(7-x)= 4 - √(3x-5 возводим обе части в квадрат и получаем
7-x = 16 - 8√(3x-5) +3x - 5 все что без корня переносим в левую часть
7 - x - 16 - 3x + 5 = -8√(3x-5)
-4-4x=-8√(3x-5)
-4(1+x)=-8√(3x-5) делим обе части на (-4), получаем
1+x=2√(3x-5) возводим обе части в квадрат, получаем
1+2x+x²=4(3x-5)
1+2x+x²-12x+20=0
x²-10x+21=0 находим дискреминант
D=100-84=16 находим корни
x=(10+4)÷2=14÷2=7
x=(10-4)÷2=6÷2=3
ответ: х=7, х=3
х км/ч - скорость катера по течению реки
у км/ч - скорость катера против течения реки
{3х + 4у = 174
{4х + 5у = 224
- - - - - - - - - -
Вычтем из первого уравнения системы второе
х + у = 50
х = 50 - у
Подставим значение х в любое уравнение системы
3 · (50 - у) + 4у = 174 или 4 · (50 - у) + 5у = 224
150 - 3у + 4у = 174 200 - 4у + 5у = 224
у = 174 - 150 у = 224 - 200
у = 24 у = 24
- - - - - - - - - -
х = 50 - 24
х = 26
ответ: 26 км/ч - скорость катера по течению реки; 24 км/ч - скорость катера против течения реки.
функция 
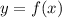не существует. То есть найдем такие значения , при которых выражение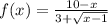 
не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
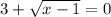, однако понятно, что 
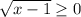, значит знаменатель не обратиться в нуль.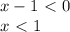
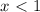функции не существует. То есть она идет от 
и куда-то дальше. Куда — нам пока неизвестно. . Может быть она периодична?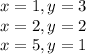 
, при котором числитель обратиться в нуль.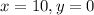 
повставлять разные значения (большие и маленькие). 
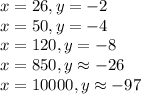
уменьшается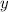 
. Делаем вывод, что функция убывает бесконечно много. То есть 
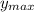— не существует, 
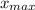— не существует. 
сначала нахочишь ОДЗ
7-х ≥0
3x+5≥0
получается x≤7
x≥5\3
следовательно допустимые x находятся в промежутки 7≥x≥5\3
теперь возводишь обе части в квадрат
7-x+2*√(7-x)*√(3x-5) +3x-5=16
2*√(7-x)*√(3x-5)=14-2x
сокращаем обе части на 2
√(7-x)*√(3x-5)=7-x
и опять возводим в квадрат обе части
(7-x)*(3x-5)=49-14x+x^2
21x-3x^2-35+5x=49-14x+x^2
4x^2-40x+84=0
сокращаем на 4
x^2-10x+21=0
дискриминант= 100-84=16
x1=(10+4)\2 x2=(10-4)\2
x1=7 x2=3
оба корня подходят
ответ: x1=7, x2=3