Прежде чем мы найдем значение выражение давайте его упростим.
(a - 3)(a + 4) - (a + 5)(a + 1).
Для открытия скобок будем использовать правило открытия скобок перед которыми стоит знак минус и правило умножения скобки на скобку.
Откроем скобки, а затем приведем подобные слагаемые.
(a - 3)(a + 4) - (a + 5)(a + 1) = a^2 + 4a - 3a - 12 - (a^2 + a + 5a + 5) = a^2 + a - 12 - (a^2 + 6a + 5) = a^2 + a - 12 - a^2 - 6a - 5 = a^2 - a^2 + a - 6a - 12 - 5 = a(1 - 6) - 17 = -5a - 17.
При а = -1/3,
-5 * (-1/3) - 17 = 5/3 - 17 = (5 - 51)/3 = -46/3 = -15 1/3.
Объяснение:
вот на
надеюсь
согласно теореме Виета
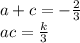
1) сложим первое уравнение и равенство a-c=6, и найдем a:
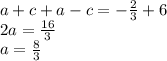
из произведения корней выразим c через k
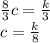
подставим c и k в равенство суммы корней
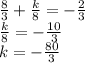
2) сложим сумму корней с равенством 3a-c=4
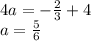
выразим c через k
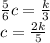
отсюда подставим в сумму корней
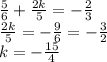
3) возведем сумму корней уравнения в квадрат
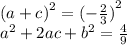
подставим заданное
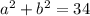
получим
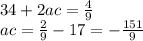
это и есть произведение корней:
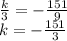
4) как в предыдущем пункте возведем в квадрат сумму корней и разделим обе части равенства на ac:
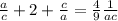
подставляем заданное отношение корней
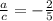
и исходное произведение корней
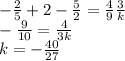
c^2+3c-c-3+6=2c^2
c^2+c^2=2c^2
2c^2=2c^2,
чтд.
значок ^ обозначает в степени