(2х-3)(2х-1)(2х+1)(2х+3)=105
применяем формулу разности квадратов
(4x^2-9)(4x^2-1)=105
16x^4-4x^2-36x^2+9=105
16x^4-40x^2-96=0
4x^4-10x^2-24=0, пусть x^2=t
4t^2-10t-24=0
D=100+384=484
Целый корень t=4, тогда х=2, х=-2
Подставим 2 в первое наше уравнение, получим
1*3*5*7=105
-7*(-5)*(-3)*(-1)=105
ответ: 1, 3, 5, 7;
-7, -5, -3, -1.
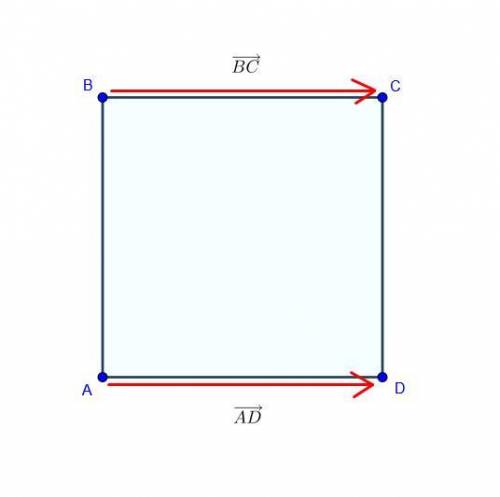
Рисунок смотрите в приложении (на нем изображены равные векторы).
Векторы равны, когда они имеют равные длины и одинаковое направление (и при этом лежат на параллельных прямых или на одной и той же прямой).а). Векторы 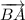 и
и 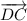 равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен
равны по модулю (то есть, равны их длины), как стороны квадрата, но имеют разное направление. Как видно из рисунка, угол между ними равен 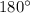 градусов (получаем, что это коллинеарные, но не равные векторы).
градусов (получаем, что это коллинеарные, но не равные векторы).
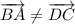 .
.
б). Векторы 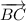 и
и 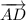 равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
равны по длине, лежат на параллельных прямых и имеют одинаковое направление. Значит, они равны.
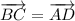 .
.
в). Векторы 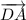 и
и 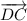 опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата -
опять же имеют одинаковые длины. Но они никак не лежат на параллельных прямых, они являются перпендикулярными (так как угол квадрата - 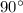 градусов).
градусов).
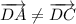
а) нет;
б) да;
в) нет.
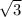 у=-5
у=-5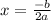
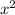 , если он положительный - ветки вверх, отриц. - ветки вниз
, если он положительный - ветки вверх, отриц. - ветки вниз
первый разложим 105 на простые множители
105=3*5*7
отсюда очевидно, что указаннным можно расписать двумя либо 105=1*3*5*7
либо 105=(-7)*(-5)*(-3)*(-1)
(число можно сколько угодно умножать на 1, если заменить хотя бы два из множителей 3, 5, 7 их произведением, то не получим последовательных нечетных чисел)
второй Пусть первое число равно 2х-3, тогда второе число равно 2х-1, третье число равно 2х+1, 2х+3
(прим.: любое нечетное число имеет вид 2n+1, где n-некоторое целое число,
два последоватьных нечетных числа отличаются значением на 2,
так 3-1=2, 7-5=2, и т.д.)
(прим. начали с 2х-3 а не с 2х+1 для простоты вычислений, в таком слычае у нас "прекрасная" возможность применить формулу разности квадратов)
по условию задачи составляему уравнение:
(2x-3)(2x-1)(2x+1)(2x+3)=105
применяя формулу квадрата разности
(4x^2-9)(4x^2-1)=106
расскрывая скобки
16x^4-4x^2-36x^2+9=105
свдя подобные члены
16x^4-40x^2+9=105
перенеся все слагаемые в левую часть
16x^4-40x^2+9-105=0
сводя подобные члены
16x^4-40x^2-96=0
разделив обе части уравнения на 8
2x^4-5x^2-12=0
введя замену
x^2=t, t>=0
получаем из биквадартного квадратное уравнение и решаем его
2t^2-5t-12=0
D=5^2-4*2*(-12)=121
t1=(5-11)/(2*2)<0 - не подходит
t2=(5+11)/(2*2)=4
откуда x=2 или х=-2
а искомые числа либо 1, 3,5 ,7 либо -7, -5, -3, -1
или (третий схожий со вторым, но с другими "заменами")если обозначать все же первое число как 2х+1, второе тогда 2х+3, третье числ о2х+5, четвертое 2х+7, получим уравнение
(2х+1)(2х+3)(2х+5)(2х+7)=105
переменожив между собой первый и четвертый множитель, второй и третий поулчим уравнение
(4x^2+8x+7)(4x^2+8x+10)=105
далее водится замена t=4x^2+8x+7
и получим квадратное уравнение
t(t+3)=105
t^2+3t-105=0
находим t1, t2
потом возвращаемся к замене и решаем четыре квадаратных уравнения
приддем к тому же результату
ответ: 1,3 ,5,7 или -7, -5, -3,-1