Разложим знаменатель на множители:
Сумма коэффициентов равна нулю, значит корни уравнения 1 и -1/3.
Интеграл примет вид:
Разложим дробь, стоящую под знаком интеграла, на составляющие:
Дроби равны, знаменатели равны, значит равны и числители:
Многочлены равны, когда равны коэффициенты при соответствующих степенях. Составим систему:
Выразим из второго уравнения А:
Подставляем в первое и находим В:
Находим А:
Сумма принимает вид:
Значит, интеграл примет вид:
Для второго слагаемого выполним приведение под знак дифференциала:
Интегрируем:
Упрощаем:
Применим свойство логарифмов:
1) 11
2) 4
Объяснение:
1) 20 + 8х - х² > 0
- х²+8x+20 = 0
D = 64+80 = 144 = 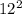
x1 = 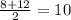 x2 =
x2 = 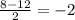
- -2 + 10 -
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток (-2; 10)
Определим целые числа в промежутке: -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Всего целых решений: 11
2) 4x² - 17x + 4 ≤ 0
4x² - 17x + 4 = 0
D = 289-64 = 225 = 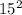
x1 = 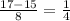 x2 =
x2 = 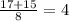
+ 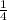 - 4 +
- 4 +
Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î Î
Нам подходит промежуток [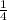 ; 4]
; 4]
Определим целые числа в промежутке: 1, 2, 3, 4
Всего целых решений: 4