{3х + 5у = 8
{-3х + у = -2
- - - - - - - - - -
Решим систему уравнений методом алгебраического сложения
0х + 6у = 6
6у = 6
у = 6 : 6
у = 1
Подставим значение у в любое уравнение системы
3х + 5 · 1 = 8 или -3х + 1 = -2
3х = 8 - 5 -3х = -2 - 1
3х = 3 -3х = -3
х = 3 : 3 х = -3 : (-3)
х = 1 х = 1
ответ: (1; 1).
Тут у меня сразу возникает несколько толкований условий задачи (какое именно увеличение имелось ввиду?).
Насколько я понимаю, в задаче подразумевался первый вариант (абсолютное увеличение зарплаты, в рублях то есть). По крайней мере, там самое простое решение и сам ответ тоже.
Остальные варианты решения приложены просто для справки (тем более, что третий вариант вообще не имеет решений).
Решение 1. Если имелось ввиду абсолютное увеличение зарплаты (т.е. на сколько рублей она увеличивалась):
Пусть первое увеличение было на x рублей
Тогда второе увеличение было на 2x рублей
Обозначим начальную зарплату как Z и составим уравнение по условиям задачи:
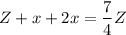
отсюда получаем:
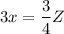
Икс равен 25 сотых от зарплаты, что соответствует 25% от зарплаты.
То есть, увеличение на x рублей означает увеличение зарплаты на 25 процентов.
ответ (для этого варианта толкования условий): в первый раз зарплата увеличилась на 25%
Решение 2. Если имелось ввиду относительное увеличение зарплаты, выраженное в процентах (т.е. на сколько процентов она увеличивалась).
Пусть первое увеличение было на x процентов (то есть, в (1+x/100) раз)
Тогда второе увеличение было на 2x процентов (то есть, в (1+x/50) раз)
Обозначим начальную зарплату как Z и составим уравнение по условиям задачи:
делим обе части на Z и получаем:
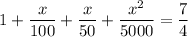
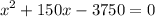
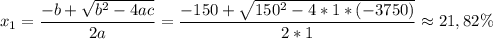
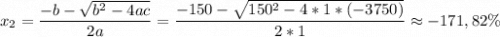(не подходит по условиям задачи, т.к. отрицательное число процентов означает уменьшение зарплаты (тут она даже ниже нуля стала бы), а в условиях сказано, что она увеличилась)
ответ (для этого варианта толкования условий): в первый раз зарплата увеличилась на 21,82%
Решение 3. Если имелось ввиду относительное увеличение зарплаты (т.е. во сколько раз она увеличивалась, коэффициент увеличения).
Пусть первое увеличение было в x раз
Тогда второе увеличение было в 2x раз
Обозначим начальную зарплату как Z и составим уравнение по условиям задачи:
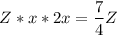
делим обе части на Z и получаем:
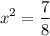
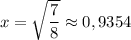(не подходит по условиям задачи, т.к. коэффициент получился меньше единицы, что означает уменьшение зарплаты, а в условиях сказано, что она увеличилась)
ответ (для этого варианта толкования условий): решений нет
