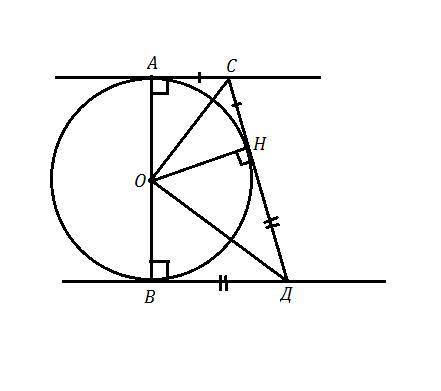
Задана окружность с центром в точке О , АВ - диаметр ,
АС и ВД - касательные к окружности, точки А и В - точки касания.
Радиус окружности, проведённый в точку касания перпендикулярен касательной ⇒ АО⊥АС и ВО⊥ВД .
СД - касательная, точка Н - точка касания ⇒ ОН⊥СД .
Получили четырёхугольник АСДВ - прямоугольная трапеция.
АС=СН и ВД=ДН , так как отрезки касательных к окружности, проведенных из одной точки, равны . ОА=ОН=ОВ как радиусы окружности, СО - общая ⇒ ΔАОС=ΔНОС , ΔВОД=ΔНОД по трём сторонам ⇒ ∠АСО=∠НСО, значит СО - биссектриса.
Рассмотрим ΔСОД. ∠СОД=90°, т.к. ∠ДСО+∠СДО=(∠С+∠Д ):2=90°
ОН - высота, опущенная из прямого угла есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой, то есть ОН²=СН*ДН , но СН=СА и ДН=ДВ, значит
ОН²=СА*ДВ
Пусть х кг - масса первого сплава, тогда
(215-х) кг - масса второго сплава.
10% от х = 0,1х (кг) - масса свинца в первом сплаве;
35% от (215-х) = 0,35(215-х)= (75,25-0,35х) (кг) - масса свинца во втором сплаве.
215 кг - масса общего сплава,
25% от 215 кг = 0,25 · 215 = 53,75 (кг) - масса свинца в общем (третьем) сплаве;
Получаем уравнение:
0,1х + (75,25-0,35х) = 53,75
0,1х + 75,25-0,35х = 53,75
0,1х - 0,35х = 53,75 - 75,25
- 0,25х = - 21,5
х = - 21,5 : (- 0,25)
х = 86
Если 86 кг - масса первого сплава, тогда
215 - 86 = 129 кг - масса второго сплава.
129 - 86 = 43 (кг)
ответ: на 43 килограмма масса первого сплава меньше массы второго.
2) = 7(1+b³)=7(1+b)(1-b+b²) = (7+7b)(1-b+b²)
3) = -x(x³-27)=-x(x-3)(x²+3x+9) = (3x-x²)(x²+3x+9)
4) = 2a(a³+125) = 2a(a-5)(a²+5a+25) = (2a²-10a)(a²+5a+25)
5) = 9a²(a³-1) = 9a²(a-1)(a²+a+1) = (9a³-9a²)(a²+a+1)