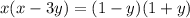. Поскольку x - простое (заметим, что 1 не считается простым числом), а произведение -(y-1)(1+y) делится на x, один из множителей делится на x. Поскольку y - простое, y не равен 1, следовательно (y-1) не равен нулю, а тогда (y-1) или (y+1) делится на x. А раз делится - не может быть меньше, чем x. Значит, по любому (y+1) больше либо равен x. Точно так же доказываем, что (x+1) больше либо равен y. Поэтому x и y могут отличаться максимум на 1.
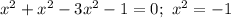- решений нет. Таким образом, решений среди простых чисел нет
{cos435
cos375}=\frac{sin810}{
cos435
cos375=\frac{90}{cos75
cos15}[\tex][tex]=\frac{1}{
cos75 cos15}=\frac{1}\frac{cos
(75-15)+cos(75+15)}{2}}=\frac{2}{cos60+cos90}=
\frac{2}{\frac{1}{2}+0}=4[\tex]