≈ 24,6°
Объяснение:
Для начала найдем вектор по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az}
AB = {3 - 3; -2 - (-1); 2 - (-3)}
AB = {0; -1; 5}
CD = {Dx - Cx; Dy - Cy; Dz - Cz}
CD = {1 - 2; 2 - (-2); 2 - 3}
CD = {-1; 4; -1}
Теперь найдем скалярное произведение векторов:
AB · CD = ABx · CDx + ABy · CDy + ABz · CDz
AB · CD = 0 · (-1) + (-1) · 4 + 5 · (-1)
AB · CD = 0 - 4 - 5
AB · CD = -9
Затем найдем длины векторов:
|AB| =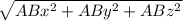 
|AB| =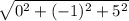 
|AB| =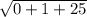 
|AB| =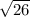 
|CD| =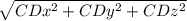 
|CD| =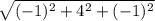 
|CD| =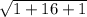 
|CD| =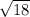 
|CD| = 3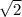
Найдем косинус угла между векторами:
cos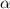 
= 
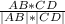
cos =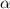 
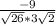
cos =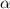 
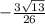
cos 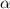= ≈ -0.41602514716892186
И наконец-то находим по таблице брадисса угол, с найденого косинуса
Это ≈ 24,6°
а)x²-2|x|+1=0
x²-2x+1=0 , x≥0
x²-2(-x)+1=0 , x≤0
x=1,x≥0
x=-1 , x≤0
x=1
x=-1
x₁=-1 , x₂=1
б)(x+1)²-6|x+1|+9=0
t²-6|t|+9=0
t=3
t=-3
x+1=3
x+1=-3
x=2
x=-4
x₁=-4 , x₂=2
в)x³+|x|=0
x³-x=0 , x≥0
x³-x=0 , x≤0
x=0
x∉R , x≥0
x=0
x=1 , x≤0
x=-1
x=0
x=-1
x₁=-1 , x₂=0
г)|x|+x+|x|×x=0
x+x+x×x=0 , x≥0
-x+x-x×x=0 , x≤0
x=0
x=-2 , x≥0
x=0 , x ≤0
x=0
x∈∅
x=0
д)|x|×x-x+2|x|-2=0
x×x-x+2x-2x-2-2=0 , x≥0
-x×x-x+2×(-x)-2=0 , x≤0
x=1
x=2 , x≥0
x=-1
x=-2 , x≤0
x=1
x=-2
x=-1
x₁=-2 , x₂=-1, x₃=1
е)x²+x+1=|x|⁰
x²+x+1=|x|⁰ , x≠0
x²+x+1=1
x²+x=0
x×(x+1)=0
x=0
x+1=0
x=0
x=-1 , x≠0
x=-1
ответ: (- 11; - 2), (7; 4)
Объяснение:
Решим второе уравнение системы:
3y² - 5y - y = 24
3y² - 6y - 24 = 0 | : 3
y² - 2y - 8 = 0
D = 4 + 32 = 36