Объяснение:
а) log₅ (x + 4) = log₅ 25
Область допустимых значений: (ОДЗ)
x + 4 > 0
x > - 4
"Опустим" логарифмы, так как у них одинаковые основания:
x + 4 = 25
x = 21
Это значение входит в ОДЗ, значит, мы получили ответ
б) log₂ (x + 2) = log₂ (x² + x - 7)
Здесь проще сразу опустить логарифмы, сделав в конце проверку для каждого корня:
x + 2 = x² + x - 7
2 = x² - 7
x² = 9
x = ±3
Для x = 3:
log₂ (3 + 2) = log₂ (9 + 3 - 7)
log₂5 = log₂5
Этот корень входит в решение.
Для x = -3
log₂ (-3 + 2) = log₂ (9 - 3 - 7)
log₂ (-1) = log₂ (-1)
Логарифма отрицательно числа не существует, значит, x = -3 не является корнем уравнения:
ответ: x = 3
в) log (1/3) (2x + 1) = -1
ОДЗ: 2x + 1 > 0
2x > - 1
x > -1/2
Вынесем степень -1 из одной третьей:
-log₃ (2x + 1) = -1
log₃ (2x + 1) = 1
Представим единицу как log₃3 и опустим логарифмы:
log₃ (2x + 1) = log₃3
2x + 1 = 3
2x = 2
x = 1
Этот корень входит в ОДЗ, значит, это наш ответ
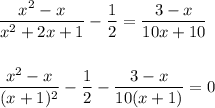
Теперь приводим дроби к одному знаменателю, который в данном случае будет равен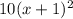 
. Для этого первую дробь мы домножаем на 10, вторую дробь - на 
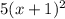, а третью - на 
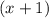. Получаем:
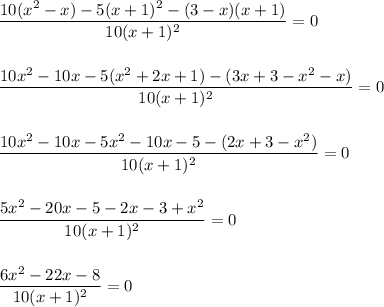
Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. То есть:
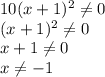
Приравняем числитель к нулю с учётом нашего условия:
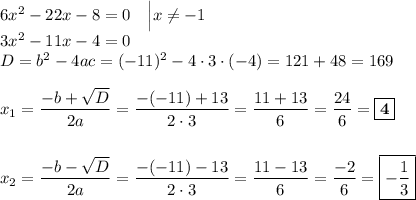
Таким образом, наше уравнение имеет два решения. Но по условию нас просят отобрать только целые решения. Наш первый корень, 4, принадлежит множеству целых чисел, в то время, как второй корень,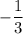 
, целым числом не является. Таким образом, в ответ пойдёт только 
.
ответ: 4.
б)y(10в квадрате +2)