Посчитаем сначала количество чисел, записываемых цифрами от 
до 
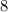, а затем из этого числа вычтем те, среди которых есть четыре идущих подряд. Сразу заметим, что если в таком числе есть четыре подряд идущих числа, то и в самом числе они должны идти подряд.
Выпишем числа от до :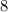 
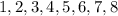. Любые 
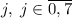вычеркнутых цифры оставят число, в котором цифры идут по возрастанию. Наоборот, любое такое число может быть получено описанной операцией. Число вычеркнуть: 
.
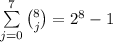Теперь посчитаем количество тех, в которых есть четыре подряд идущих. В этом случае мы можем вычеркивать только из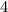 
-ех оставшихся чисел. Поскольку четверок подряд идущих 
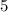, то всего искомых чисел 
.
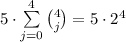Итого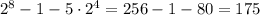 
.
Пусть один катет будет Х а второй У. До изменения катетов площадь была 24 то есть (Х*У)/2 = 24 - это согласно формуле площади прямоугольного треугольника, которая говорит что площадь прямоугольного треугольника это перемноженные катеты и поделенные на два. Далее один катет уменьшили на 1 то есть Х-1, а второй увеличили на 3 то есть У+3 и теперь площадь стала 27,5 то есть (Х-1)*(У+3) / 2 = 27,5
(Х*У)/2 = 24
(Х-1)*(У+3) / 2 = 27,5
Дальше раскрываете второе уравнение и решаете методом подстановки. Если не ошибаюсь получится квадратное уравнение, кторое решается через дискриминант. Вы уже проходили квадратные уравнения? Справитесь? Другого решения я не знаю...
Решение
1.
а) S(t) = 2t - 1;
Механический смысл производной: S`(t) = V(t)
S`(t) = 2
б) S(t) = 4t - 3
S`(t) = 4
2. Найдите скорость изменения функции f(x) = 2x^2 (два икс в квадрате) в точке x0 = 2 (икс нулевое равно двум)
V(x) = f`(x) = 4x
x0 = 2
V(2) = f`(2) = 4*2 = 8
3 .
Найдите скорость и ускорение движения точки в момент времени t = 2, если её закон движения по прямой задан формулой S(t) = 2t^2 + 3t.
V(t) = S`(t) = 4t + 3
V(2) = 4*2 + 3 = 11
a(t) = V`(t) = 4