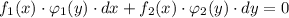
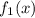и 
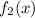зависят только от переменной "х" , а функци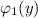и 
и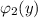 
зависят только от переменной "у" . Указывается на то, что диффер. уравнение допускает обособление (разделение) переменных только тогда, когда перед дифференциалами (dx и dy) стоят функции, являющиеся произведениями двух других функций, одна из которых зависит только от "х" , а вторая зависит только от "у" . 
. 
.
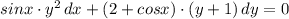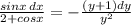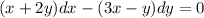, то переменные уже нельзя разделить, так как нельзя функции, стоящие перед dx и dy,представить в виде произведения 
.
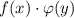2x^2+6x-4=0
x^2+3x-2=0
D=3^2-(-4*(1*2))=17
x=-корень(17)/2-3/2,
x=корень(17)/2-3/2
2.
4x^2-100=0
4x^2=100
x^2=25
D=(0)^2-(4*4*(-100)=1600
x=-5
x=5
3.
6x^2+5x=0
x*(6x+5)=0
6x=-5
D=(5)^2-(4*6*0)=25
x+-5/6
x=0