
1. с) 4 см.
2. d) 14 см.
3. в) 8 см.
Объяснение:
". Основание равнобедренного треугольника равно 10 см., а боковая сторона 8 см. чему равна длина отрезка, соединяющего середины основания и боковой стороны?"
***
АВС - треугольник. АВ=ВС=8 см. MN - средняя линия треугольника MN║AB и равно его половине МН=АВ/2=8/2=4 см.
***
"В квадрате с диагональю 7 см последовательно соединили отрезками середины сторон. Найдите периметр образованного четырехугольника."
***
ABCD - квадрат. АС=7 см - диагональ квадрата.
Соединили середины сторон квадрата. Получили квадрат A1B1C1D1? стороны которого являются средними линиями диагоналей квадрата и равны его половине.
A1B1=B1C1=C1D1=A1D1=AC/2=7/2=3.5 см .
Р=4А1В1=4*3,5=14 см.
***
3. Средняя линия треугольника параллельна основанию и равна его половине.
АВС - равносторонний треугольник. MN =4 см - средняя линия. MN║AC. MN=AC/2. AC=2*MN=8 см .
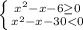
1) x² - x - 6 ≥ 0
(x - 3)(x + 2) ≥ 0
+ - +
______[- 2]______[3]_______
////////////// ////////////////
x ∈ (- ∞ ; - 2] ∪ [3 , + ∞)
2) x² - x - 30 < 0
(x - 6)(x + 5) < 0
+ - +
_______(- 5)______(6)______
///////////////////
x ∈ (- 5 ; 6)
Окончательно :
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ /////////////////////////
______(- 5)_____[- 2]_______[3]_____(6)_____
////////////////////////////////////////////////
ответ : x ∈ (- 5 ; - 2] ∪ [3 ; 6)