
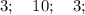
Объяснение:
6) Так как произведение корней принимает положительное значение, то и сами корни принимают положительные значения ⇒ подкоренные выражения также положительны.
ОДЗ:
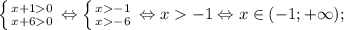
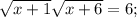
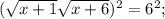
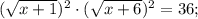
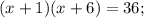
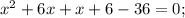
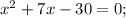
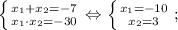
Корень x₁ не удовлетворяет ОДЗ.
7) Знаменатель дроби не равен нулю ⇒ подкоренное выражение строго больше 0. Подкоренное выражение правой части уравнения также строго больше 0, поскольку, в противном случае, значение числителя равно 0, отсюда выходит, что "х" принимает отрицательное значение, что противоречит ОДЗ подкоренного выражения знаменателя дроби.
ОДЗ:
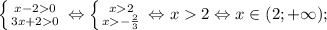
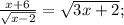

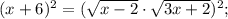

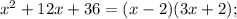
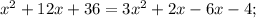
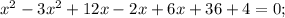
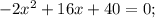
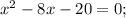
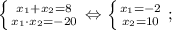
Корень x₁ не удовлетворяет ОДЗ.
8) ОДЗ:

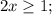
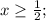
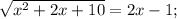
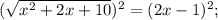
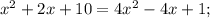
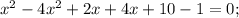
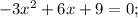
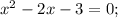
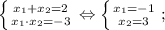
Корень x₁ не удовлетворяет ОДЗ.
1) Обозначим первую цифру задуманного числа х, а вторую - у. Выполнив указанные действия, получим:
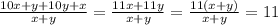
Т.е., всегда будет получаться 11.
2) Признак делимости на 3: на три делятся те числа, сумма цифр которых делится на 3.
Данное число (10^n+317) будет состоять из единицы, n нулей, тройки, единицы и семёрки. Сумма цифр равна 1+3+1+7 = 12.
12 делится на 3, значит, и число 10^n+317 тоже делится на 3, ЧТД
Аналогично, признак делимости на 9: на 9 делятся те числа, сумма цифр которых делится на 9.
10^n состоит из единицы и n нулей. Если от него отнять 1, оно будет состоять из девяток. Соответсвенно, сумма цифр этого числа поделится на 9, ЧТД.