Пусть первое число равно х, тогда второе число равно (17 - х). Квадрат первого числа равен х^2, а квадрат второго числа равен (17 - х)^2. По условию задачи известно, что сумма квадратов этих двух чисел равна (х^2 + (17 - х)^2) или 185. Составим уравнение и решим его.
х^2 + (17 - х)^2 = 185;
х^2 + 289 - 34х + х^2 = 185;
2х^2 - 34х + 289 - 185 = 0;
2х^2 - 34х + 104 = 0;
х^2 - 17х + 52 = 0;
D = b^2 - 4ac;
D = (-17)^2 - 4 * 1 * 52 = 289 - 208 = 81; √D = 9;
x = (-b ± √D)/(2a);
x1 = (17 + 9)/2 = 26/2 = 13 - первое число;
х2 = (17 - 9)/2 = 8/2 = 4 - первое число;
17 - х1 = 17 - 13 = 4 - второе число;
17 - х2 = 17 - 4 = 13 - второе число.
Нехай за 
год перший робітник виконає завдання, а за 
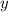год — другий. Тоді за одну годину перший робітник виконає 
усього завдання, а другий робітник — 
.
Два робітники, працюючи разом, можуть виконати завдання на 8 год швидше, ніж один перший робітник, тобто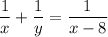 
Два робітники, працюючи разом, можуть виконати завдання на 18 год швидше, ніж один другий робітник, тобто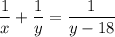 
Складаємо систему з двох рівнянь:
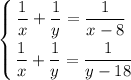
Тут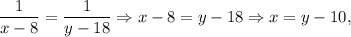 
оскільки ліві частини рівнянь рівні.
Підставимо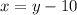 
в перше рівняння:
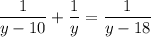
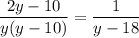
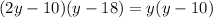
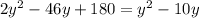
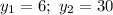
Якщ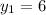о 
, то 
— не відповідає сенсу задачі.
Якщ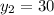о 
, то 
Отже, за 20 год перший робітник виконає завдання, а за 30 год — другий.
Відповідь: 20 год і 30 год.
