Формативное оценивание по алгебре в 7 классе — это процесс оценки знаний и умений учеников на уроке или в течение учебного года с целью определить их прогресс и повысить качество обучения. Формативная оценка основывается на оценке учебных достижений учащихся в различных областях алгебры.
На приведенной таблице представлены различные области алгебры, такие как "Формулы", "Решение уравнений" и "Графики". Ниже каждой области указаны оценки: "1", "2", "3" и "4", которые представляют соответственно "неудовлетворительно", "удовлетворительно", "хорошо" и "отлично".
Для каждой области алгебры ученик получает оценку, основанную на его знаниях и умениях, продемонстрированных в ходе урока или учебной работы. Подробный ответ и объяснение для каждой оценки приведены ниже.
1. Область "Формулы":
- Оценка "1" (неудовлетворительно): Ученик не может составить и применить алгебраические формулы для решения простых задач.
- Оценка "2" (удовлетворительно): Ученик может составить и использовать простые алгебраические формулы для решения задач, но с некоторыми ошибками.
- Оценка "3" (хорошо): Ученик может составить и применить алгебраические формулы для решения большинства задач без существенных ошибок.
- Оценка "4" (отлично): Ученик может составить и использовать сложные алгебраические формулы для решения разнообразных задач без ошибок.
2. Область "Решение уравнений":
- Оценка "1" (неудовлетворительно): Ученик не понимает, как решать уравнения и не может применять соответствующие методы.
- Оценка "2" (удовлетворительно): Ученик может решать простые уравнения с некоторыми ошибками или подсказками.
- Оценка "3" (хорошо): Ученик может решать разнообразные уравнения без существенных ошибок.
- Оценка "4" (отлично): Ученик может решать сложные уравнения с использованием различных методов без ошибок.
3. Область "Графики":
- Оценка "1" (неудовлетворительно): Ученик не может строить графики, интерпретировать и использовать основные элементы графиков.
- Оценка "2" (удовлетворительно): Ученик может строить простые графики и делать простые выводы на основе них, но с некоторыми ошибками.
- Оценка "3" (хорошо): Ученик может строить и анализировать сложные графики без существенных ошибок.
- Оценка "4" (отлично): Ученик может строить сложные графики и делать сложные выводы на основе них без ошибок.
Это формативное оценивание поможет учителю и ученикам определить области, в которых учащемуся нужно больше работать и улучшать свои знания и навыки. Ученики также смогут видеть свой прогресс в учебе и знать, на чем нужно сосредоточиться для улучшения успехов по алгебре.
Для определения области определения функции нужно найти значения аргумента (х) в которых функция определена, то есть значения, при которых подкоренное выражение внутри функции неотрицательно.
В данном случае у нас есть функция у = √(4 - 13х + 3х^2)
Для того чтобы подкоренное выражение было неотрицательно, должно выполняться условие:
4 - 13х + 3х^2 ≥ 0
Это квадратное неравенство мы можем решить, найдя его корни. Но сначала перепишем его в виде квадратного уравнения:
3х^2 - 13х + 4 = 0
Чтобы решить это уравнение, воспользуемся квадратным уравнением в общем виде:
x = (-b ± √(b^2 - 4ac)) / (2a)
В нашем случае, a = 3, b = -13, c = 4.
x = (-(-13) ± √((-13)^2 - 4*3*4)) / (2*3)
x = (13 ± √(169 - 48)) / 6
x = (13 ± √121) / 6
x = (13 ± 11) / 6
Получили два значения аргумента:
x1 = (13 + 11) / 6 = 24 / 6 = 4
x2 = (13 - 11) / 6 = 2 / 6 = 1/3
Таким образом, область определения функции у = √(4 - 13х + 3х^2) - это все значения x, которые могут быть равны 4 или 1/3.
Если у школьника остаются вопросы или не все шаги понятны, я могу объяснить еще более детально.
А — выиграть главный приз;
Сумма вероятностей события и его отрицания есть достоверное событие, то есть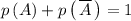
где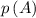 - вероятность выигрыша главного приза;
- вероятность выигрыша главного приза;
ответ: