
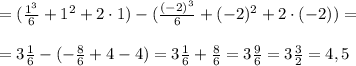
Решение
Пусть x км/ч - скорость мотоциклиста,
(60/x) ч время, затраченное от села до озера
(х -10) км/ч - скорость на обратном пути,
60/(x - 10) ч время, затраченное на обратный путь
60/x меньше 60/(x - 10) на 0,3
Составим и решим уравнение:
60/(x-10) - 60/x = 0,3
600x - 600x +6 000 = 3x² - 30x
3x² - 30x - 6000 = 0 делим на 3
x² -10x – 2000 = 0
D = 100 + 4*1*2000 = 8100
x₁ = (10 - 90)/2 = - 40 < 0 не удовлетворяет условию задачи
x₂ = 10 + 90)/2 = 50
60/(50-10) = 60/40 = 1,5 ч - время, затраченное на обратный путь
ответ: 1,5 ч
Решение
Пусть x км/ч - скорость мотоциклиста,
(60/x) ч время, затраченное от села до озера
(х -10) км/ч - скорость на обратном пути,
60/(x - 10) ч время, затраченное на обратный путь
60/x меньше 60/(x - 10) на 0,3
Составим и решим уравнение:
60/(x-10) - 60/x = 0,3
600x - 600x +6 000 = 3x² - 30x
3x² - 30x - 6000 = 0 делим на 3
x² -10x – 2000 = 0
D = 100 + 4*1*2000 = 8100
x₁ = (10 - 90)/2 = - 40 < 0 не удовлетворяет условию задачи
x₂ = 10 + 90)/2 = 50
60/(50-10) = 60/40 = 1,5 ч - время, затраченное на обратный путь
ответ: 1,5 ч
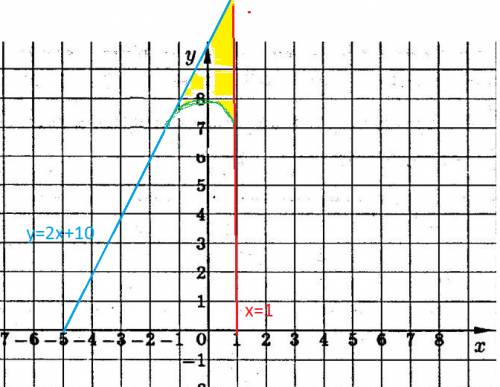
Уравнения касательной функции y = 8 - 0,5x² в точке с абсциссой xo= -2.
y -yo = y '(xo)*(x-xo); || yo =y(xo)_значения функции в точке xo = -2||
yo =8 -0,5(-2)² =8 -2 =6 ;
y ' =( 8 -0,5x²) ' = -x ⇒ y'(xo)= y ' | x=xo = -(-2) =2.
y -6 =2(x -(-2))⇔ y =2x +10.
1 1
S = ∫ (2x+10 -(8 -0,5x²)dx = ∫ (0,5x²+2x+2)dx =
-2 -2
(x³/6 +x² +2x) | a =-2 , b= 1 =1³/6 +1³+2*1 -( (-2)³/6 +(-2)² +2*(-2) ) =
= 4,5.