График-это взаимосвязь оси Ох и оси Оу. то есть ,что бы получить график выбираем значение Х или У и решаем по формуле. в твоем случае формула -это y= 20x^2. то есть любая точка, принадлежащая графику, должна входить в уравнение. пример: берем любое точку на графике(ну в данном случае это парабола) . Находим по графику Х и У. подставляем в уравнение-решаем. должно получится что У будет равен Х. например: берем точку, у=100 , а х= 0.5 . подставляем:
100=20×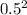
100=100-верно. точка принадлежит графику.
Обозначим скорость течения через х, тогда
16+х - скорость катера по течению,16-х - скорость против течения
9/(16+х)- время катера по течению
21/(16-х)- время катера против течения
Запишем в виде уравнения:
9/(16+х)+21/(16-х)=2 часа
Приведем все к общему знаменателю (16+х)(16-х)=256-х^2 и уберем занменатель, получим:
9*(16-х)+21*(16+х)=2*(256-х^2)
Упрстим:
144-9х+339+21х=2*256-2* х^2
12х+ 2* х^2-32=0
х^2+6х-16=0
Через дискриминант(=100) находим корни уравнения:
х1=2 х2=-8
х2 нам не подходит, так как имеет отрицательное значение
Значит скорость течения 2 км/ч
Нажми, чтобы рассказать другим, насколько ответ полезен
Подробнее - на -
Они встретились на расстоянии 28 км от середины.
Таким образом, 1 поезд проехал S/2 - 28 км, а 2 поезд S/2 + 28 км за одинаковое время.
t1 = (S/2 - 28)/x = (S/2 + 28)/(x+10)
Если бы 1 поезд выехал на 45 мин = 3/4 часа раньше 2 поезда,
то он успел бы проехать 3x/4 км, в то время как 2 поезд только выехал.
В таком случае они встретились бы посередине.
t2 = (S/2 - 3x/4)/x = (S/2)/(x+10)
Можно составить систему из этих уравнений
{ (S/2 - 28)/x = (S/2 + 28)/(x+10)
{ (S/2 - 3x/4)/x = (S/2)/(x+10)
Решение:
{ (S-56)(x+10)/(2x(x+10)) = (S+56)*x/(2x(x+10))
{ (2S-3x)(x+10)/(4x(x+10)) = (2Sx)/(4x(x+10))
{ Sx - 56x + 10S - 560 = Sx + 56x
{ 2Sx - 3x^2 + 20S - 30x = 2Sx
{ 10S = 112x + 560
{ -3x^2 + 20S - 30x = 0
{ S = 11,2x + 56
{ -3x^2 + 20(11,2x + 56) - 30x = 0
3x^2 - 224x + 30x - 1120 = 0
3x^2 - 194x - 1120 = 0
x1 < 0
x2 = 70
Итого, x = 70 - скорость 1 поезда, x+10 = 80 - скорость 2 поезда,
S = 11,2x + 56 = 11,2*70 + 56 = 840 км.