Нужно найти предел суммы ряда. первое что приходит в голову вынести : nx/4n^2*x^2=1/4nx за знак суммы , тогда внутри суммы k=0 до k=n остается выражение:
1/(1/x^2 +(k/2n)^2) , нет смысла стараться (у вас явно ничего не получится) найти сумму такого ряда.теперь есть вопрос, можно ли рассуждать следующим образом или все вышесказанное является несправедливым? возьмем какой нибудь бесконечно большой номер k=m после которого будет считать , что k=m соизмеримо по размеру с n (k=n-i ,где i-конечное целое число) , в этом случае предел :
lim k/n =lim(n-i)/n=1 i-конечное целое число . равен 1 , а для всех остальных k для которых i -бесконечно большое этот предел будет равен 0. таким образом сумма этого ряда при cтремлении n к бесконечности будет равна: (n-m+1)*(1/(1/x^2 +(1/2)^2) +(m-1)*(1/x^2) = x^2*( m-1 +4*(n-m+1)/(4+x^2) ). теперь учтем вынесенный за скобки множитель : 1/4*n*x * x^2*( m-1 +4*(n-m+1)/(4+x^2) ) учитываем что при стремлении n к бесконечности : (m-1)/n=1 ; (n-m+1)/n=(1-1)/1=0
тогда искомый предел равен: x^2/4x= x/4 . вывод: предел равен x/4. если я не прав и этот не является ,,честным'' решите так как нужно. потому что других идей я тут придумать не смог. может есть какая-то теорема о которой я не слышал , что сможет решить эту .



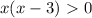
 ∈
∈ 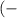 ∞
∞  ∪
∪ 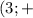 ∞
∞ 

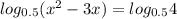
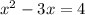
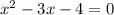
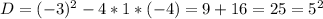
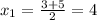
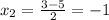



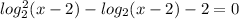

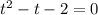

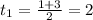

 или
или 
 или
или 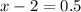
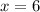 или
или 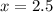

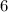
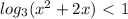

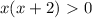
 ∈
∈ 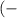 ∞
∞  ∪
∪ 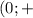 ∞
∞ 

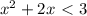


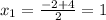

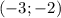 ∪
∪ 
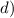
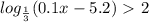







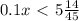



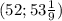
У вас были определенные интегралы? Если да, то:
(т.к. это с точностью до одного слагаемого интегральная сумма; значения функции берутся на отрезке [0,1] в точках k/n)
Т.е. ответ: 1/2 arctg(x/2)
На всякий случай проверил численно, при n = 10000 и x = 1, 2, 3 значения суммы ряда и получившейся предельной функции равны соответственно:
0.231846 0.231824
0.392736 0.392699
0.491446 0.491397