Термин "сократить" употребляется только для сокращения МНОЖИТЕЛЕЙ. В числителе заданной дроби стоит выражение, которое называется алгебраическая СУММА, но не произведение. Поэтому ничего нельзя сокращать.
Причём в этой сумме есть слагаемое, которое представляет из себя произведение (2х+1)(х+1) , но всё же оно СЛАГАЕМОЕ, но не произведение. Если бы числитель был полностью разложен на множители, то тогда сократить можно было бы одинаковые МНОЖИТЕЛИ.
Здесь можно было почленно разделить слагаемые числителя на знаменатель, и тогда появиться дробь, где в числителе будет стоять произведение, в котором одним из множителей будет (2х+1) , который есть и в знаменателе. Вот в этой дроби и можно сократить одинаковые множители.
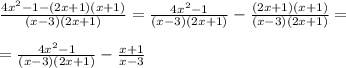
Дана функция y=x^4-2x^3+3.
Её производная равна: y' = 4x³- 6x².
Приравняем производную нулю:
4x³- 6x² = 2x²(2х - 3) = 0.
Отсюда находим 2 критические точки (они же стационарные):
х = 0 и х = 3/2.
Они разбивают область определения функции на 3 промежутка:
(-∞; 0), (0; 3/2)) и ((3/2); +∞).
Определяем свойства полученных точек по знаку производной в найденных промежутках.
х = -1 0 1 3/2 2
y' = -10 0 -2 0 8 .
Как видим, есть только одна точка экстремума-это минимум функции в точке х = 3/2.
(80; 4) и (2,5; -16)
Объяснение:
Решение во вложении.