Самым семейным, теплым и радостным праздником считается Новый год. Каждый человек ждет новогоднего волшебства. Многие верят, что новогодняя ночь исполняет все желания. Особенно ждут этот праздник дети, ведь именно им Дедушка Мороз приносит много интересных подарков. Люди посылают новогодние открытки своим родственникам и друзьям, а также делают друг другу сюрпризы.
Весь город готовится к этому волшебному празднику. Зимние улицы украшают разноцветными гирляндами и флажками. Повсюду раздается звон колокольчиков. В домах наряжают новогодние елочки, которые вместе с Дедом Морозом и Снегурочкой являются самыми главными символами Нового года. Опутанные нитями бус, в праздничной мишуре и сверкающих шарах, они красуются в каждой семье. На макушках обязательно горят яркие звездочки.Детишки старательно пишут Деду Морозу свои о подарках, которые хотели бы получить. Они верят, что Дедушка Мороз и его внучка Снегурочка приезжают из леса на санях, запряженных тройкой резвых лошадей. Все с азартом готовятся к долгожданному празднику. Ребята мастерят себе костюмы различных сказочных персонажей и лесных зверей. Детки рассказывают Дедушке Морозу и Снегурочке стихотворения, поют песенки, водят хороводы у наряженной новогодней красавицы елки, за что получают заслуженные подарочки от Деда Мороза.
Празднование Нового года на этом не заканчивается, а продолжается в семейном кругу. 31 декабря вся семья собирается вместе у праздничного стола. Ещё один плюсВсе начинают поздравлять друг друга, желать здоровья, счастья и успехов. Ведь именно Новый год является всеобщим сказочным праздником. Он дарит всем нам веру во что-то новое, светлое и интересное. Все плохое, старое и ненужное, остается в году. Ранним утром каждый ребенок находит под елочкой желанный подарок и сожалеет, что снова нечаянно проспал визит Дедушки Мороза. Нового года в том, что это самый вкусный праздник В эти самые минуты, затаив дыхание, все загадывают желания. Очень важно верить в то, что они, несомненно, сбудутся.разными блюдами. Все люди ожидают с полуночи, когда под бой курантов начинается настоящее веселье.
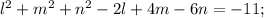
добавим к обоим частям уравнений +1 +4 +9 и перегруппируем так, чтобы видеть квадраты двучленов
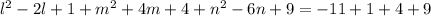
теперь выделяем квадраты
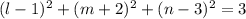
так как l, m, n целые числа, то целыми будут числа l-1,m+2,n-3 и их квадраты, при этом квадраты равны либо 0 либо 1 (квадраты целых чисел либо 0 либо натуральное число) потому что если хотя бы один из квадратов равен 4=2^2 или больше то л.ч.уравнения больше за правую и искомых троек чисел не существует
но так как из всех возможных 8 сумм из 0 и 1, только 1+1+1=3
то 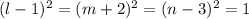
откуда l-1=1 или l-1=-1
m+2=1 или m+2=-1
n-3=1 или n-3=-1
значит l=2 или l=0, m=-1 или m=-3, n=4 или n=2
итого восемь пар решений (l;m;n)
(2;-1;4)
(2;-1;2)
(0;-1-;4)
(0;-1;2)
(2;-3;4)
(2;-3;2)
(0;-3;4)
(0;-3;2)
вторая задача
обозначим учеников через 1,2,..8, а кружки через А,Б,В,Г,Д
не ограничивая общности если 1й ходит только в кружок А, то остальные в кружок А ходить не могут, иначе сразу противоречие (если например второй ходит в кружок А и другой кружок, например Б, то он ходит во все кружки в которые ходит 1, что невозможно)
т.е. ученики ходят минимум в 2 кружка (могут и в большее).
никто из ребят не может ходить сразу во все пять кружков, иначе он будет ходить во все кружки которые ходит любой другой из ребят
Далее если например 1й ученик ходит в 4 кружка (например А,Б,В,Г), то
никто не может ходить в комбинацию двух или трех кружков из кружков А,Б,В, Г так как 1й будет ходить во все кружки что и второй
остаются возможными варианты Б,Е или В,Е, или Г,Е или А,Е или А,Б,Е, или Б, В, Е, или В,Г, Е, или А,Г,Е или Б, В, Г, Е или А, Б, В, Е, или А,Г, В, Е или А, Б, Г, Е
если 2й ходит в 2 кружка из оставшихся например Б,Е , то исключая противоречивые согласно условию остаются возможными 6 вариантов или В,Е, или Г,Е или А,Е или В,Г, Е, или А,Г,Е или А,Г, В, Е (среди которых есть противоречивые например В,Е и А,Г, В, Е) и вариантов получается меньше чем 6, и для какогото из учеников не остается варианта выбора
если 2й ходит в 3 кружка, например А,Б,Е, то исключая остаются возможности для других учеников или В,Е, или Г,Е или В,Г, Е, или А,Г,Е или Б, В, Г, Е или А,Г, В, Е - 6 возможностей , среди которых есть противоречивые (например Г,Е и А,Г, В, Е) и возможностей получается меньше чем оставшихся учеников.
если 2й ходит в 4 кружка например Б, В, Г, Е, то исключая согласно условию остаются возможности или А,Б,Е или А,Г,Е или А, Б, В, Е, или А,Г, В, Е или А, Б, Г, Е - 5 возможностей - меньше чем оставшихся учеников. Следовательно и такой вариант событий не подходит.
Таким образом получаем что не один ученик не может ходить в четыре кружка.
Обьединяя получаем искомое, что согласно правилам и условию каждый школьник занимается в 2х или 3х кружках.
такое возможно
например
1 - А,Б, 2 - Б,В, 3 - В,Г, 4 - Г,Д, 5 -Д,Е 6 - А,Е, 7 - Б,Е 8 - Г,Е