
ответ: 8/√3 (ед.длины)
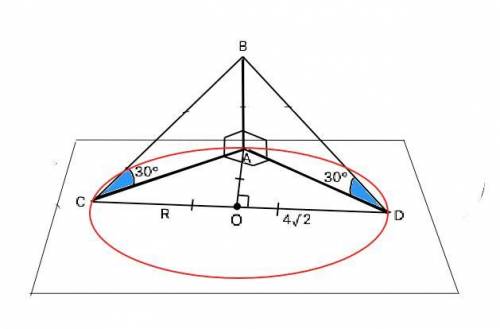
Объяснение: АВ перпендикулярно плоскости альфа ⇒АВ перпендикулярно любой прямой, лежащей в этой плоскости ⇒ АВ⊥АС и АВ⊥АD.
Треугольники АВС и ∆АВD имеют по равному острому углу (дано) и общему катету АВ, следовательно, они равны. из чего следует равенство катетов прямоугольного ∆ АСD, т.е. АС=АD и углы АСD=ADC=(180°-90°):2=45°.
Центром окружности, описанной около прямоугольного треугольника, является середина его гипотенузы. R=CO=DO=4√2. ⇒ медиана АО=R=4√2, а
АС=СО/sin45°=4√2)/√3/2=8 (ед. длины)
Из прямоугольного ∆ АВС катет АВ=АС•tg30°=8•1/√3=8/√3
5(х-1/5)(х+4)=0 (:5)
(х-1/5)(х+4)=0
х-1/5=0 х=1/5 х=0,2
х+4=0 х=-4
(х-0,2)(х+4)>0
-4 0,2 x
+ - +
смотрим промежутки со знаком +, так как >0
x∈(-∞;-4)∪(0,2;+∞)